Розвинення функцій в степеневі ряди

Якщо функція має в точці і деякому її околі похідні до 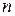-го порядку включно, то в кожній точці цього околу вона представлена| формулою Тейлора:

(1)

де – залишковий член формули Тейлора, який може бути записаний у вигляді

(форма Пєано). (2)

Запис (10) означає, що , тобто що залишковий член формули Тейлора є нескінченно мала вищого порядку малості в порівнянні з при .

Якщо функція має в згаданім околі точки безперервну похідну -го порядку, то залишкового члена формули Тейлора можна записати в наступних трьох виглядах:

(форма Лагранжа);

(форма Коші);

(інтегральна форма).

Нехай тепер функція має в точці і деякому її околі похідні всіх порядків. Тоді число членів формули (1) можна необмежено збільшувати і виникає питання: чи не одержимо ми в границі при подану функцію у вигляді ряду

(3)

Ряд (9) незалежно від того, збігається він до функції чи ні, називається рядом Тейлора для функції . Якщо ж для всіх значень з деякого околу точки має місце рівність

(4)

то функція називається розкладною в ряд Тейлора в околі точки (або за ступенями ). При 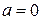ряд Тейлора має вигляд

(5)

і називається рядом Маклорена.