 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пределы
|
|
Рассмотрим наиболее важные для практики пределы:
1. Если функция 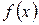 определена в точке x = x 0, то
определена в точке x = x 0, то 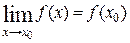 ; 2.
; 2. 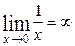 ;
;
3. 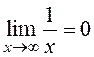 ; 4.
; 4. 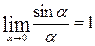 – первый замечательный предел;
– первый замечательный предел;
5. 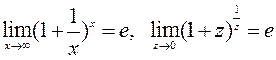 – второй замечательный предел (
– второй замечательный предел (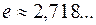 );
);
6.  ; 7.
; 7. 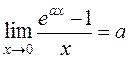 .
.
Примеры. Найти пределы функций.
1. 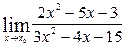 при а) х 0 = 3; б) х 0 = ¥.
при а) х 0 = 3; б) х 0 = ¥.
2. 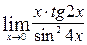 ; 3.
; 3. 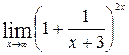 .
.
Решение:
1. а) 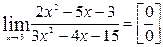 .
.
Подстановка предельного значения аргумента х 0=3 приводит к неопределенности вида 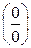 .
.
Для раскрытия получившейся неопределенности найдем корни числителя: х 1=3 и х 2= 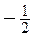 ; и корни знаменателя: х 1=3 и х 2=
; и корни знаменателя: х 1=3 и х 2= 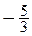 . Тогда применяя формулу
. Тогда применяя формулу
ах 2 + bх+с=а (х-х 1)(х-х 2), получим:
2 х 2 - 5 х- 3 = 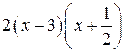 = (х- 3)(2 х+ 1);
= (х- 3)(2 х+ 1);
3 х 2-4 х -15= 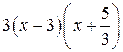 =(х -3)(3 х +5).
=(х -3)(3 х +5).
После преобразования числителя и знаменателя, и сокращения дроби на (х –3) (до перехода к пределу), повторяем непосредственную подстановку предельного значения.
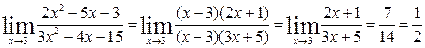 .
.
б) 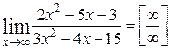 .
.
При х ®¥ получаем неопределенность 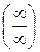 . Для раскрытия неопределенности разделим многочлены числителя и знаменателя на старшую степень аргумента, т. е. на х 2.
. Для раскрытия неопределенности разделим многочлены числителя и знаменателя на старшую степень аргумента, т. е. на х 2.
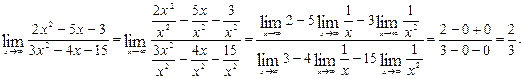
2. 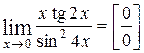 .
.
При вычислении пределов от тригонометрических функций обычно применяется первый замечательный предел: 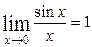 .
.
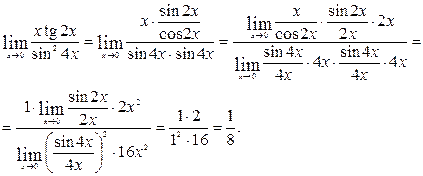
3. 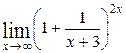 =
= 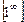 .
.
Для того, чтобы применить второй замечательный предел, воспользуемся подстановкой t=х +3. Тогда x = t –3, 2 x =2 t –6 и, если 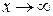 , то и
, то и 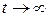 .
.
Таким образом,
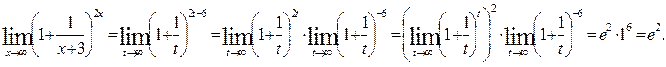
Дата публикования: 2014-10-20; Прочитано: 417 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
