Решение. Найдем производную данной функции:

1. .

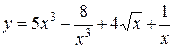Найдем производную данной функции:

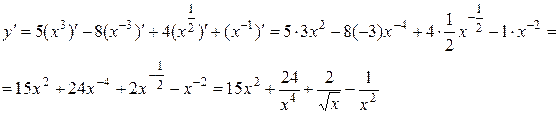
Так как дифференциал функции 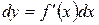, получим:

.

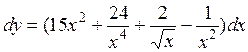2. .

Найдем производную данной функции:

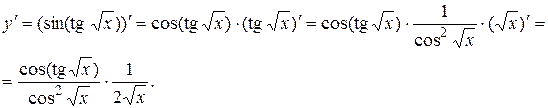
Следовательно, .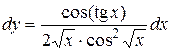

3. .

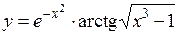Найдем производную данной функции. Применяем формулу (2.1) производной произведения двух функций,

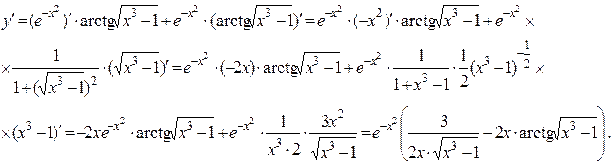
Следовательно, .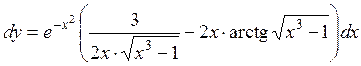

4. .

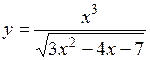Найдем производную данной функции. Применяем формулу (2.2) производной частного двух функций,

.

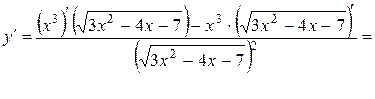
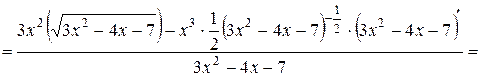
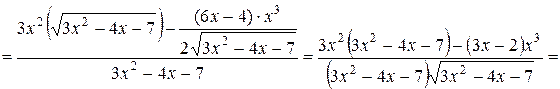
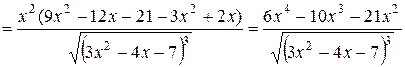Следовательно, .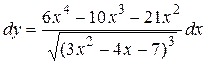

Пример. Составить уравнение касательной и нормали к кривой 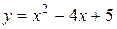в точке .

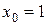Найдем значение функции в точке x ₀, 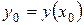; производную функции 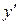и значение производной в точке x ₀, :

; ; .

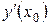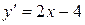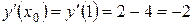Так как уравнение касательной, проходящей через т. 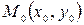, имеет вид

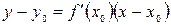, получим:

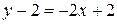; или .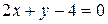

Уравнение нормали, проходящей через т. 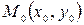, имеет вид

.

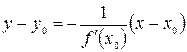Для рассматриваемого случая получим:

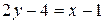; или .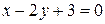

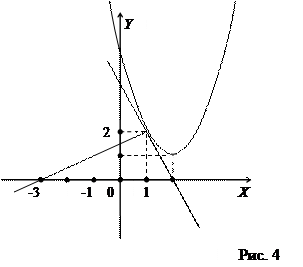
Сделаем чертеж (рис. 4).

Уравнение данной линии запишем в виде 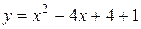или 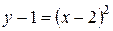. Это парабола с вершиной в точке (2, 1) и осью симметрии, параллельной оси ОУ.