 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Производная фунции и её геометрический смысл
|
|
Пусть c=const, u=u (x), v=v (x)некоторые дифференцируемые функции, тогда справедливы следующие правила дифференцирования:
1.  ; 4.
; 4.  ; (2.1)
; (2.1)
2.  ;5.
;5.  (2.2)
(2.2)
3.  ; 6.
; 6.  ;
;
если 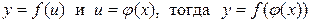 — сложная функция аргумента х и
— сложная функция аргумента х и
 или
или  .
.
На основании определения производной и правил дифференцирования составлена таблица производных основных элементарных функций.
1.  где где 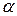 — любое действительное число — любое действительное число
| 2.  ; ;
|
3.  ; ;
| 4.  ; ;
|
5.  ; ;
| 6.  ; ;
|
7. 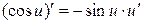 ; ;
| 8.  ; ;
|
9.  ; ;
| 10.  ; ;
|
11.  ; ;
| 12.  ; ;
|
13.  . .
|
B приведенной таблице основных формул дифференцирования функций, переменная u может быть как независимой переменной, так и некоторой функцией от другой переменной.
Примеры. Найти дифференциалы функций:
1. 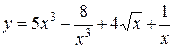 ; 2.
; 2.  ; 3.
; 3.  ;
;
4. 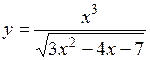 .
.
Дата публикования: 2014-10-20; Прочитано: 373 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
