|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Непрерывность функции. Определение. Функция называется непрерывной в точке х = х0 , если она в этой точке определена и
|
|
Определение. Функция 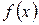 называется непрерывной в точке х = х 0, если она в этой точке определена и
называется непрерывной в точке х = х 0, если она в этой точке определена и 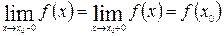 .
.
Пример. Исследовать на непрерывность функцию
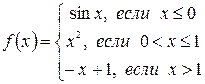 .
.
Построим график этой функции (рис. 3).
|
Данная функция состоит из трех аналитических выражений, каждое из которых непрерывно в своей области. Поэтому функция может иметь разрывы только в местах перехода от одного аналитического выражения к другому, т.е. в точках х =0 и х =1.
Исследуем эти точки:
а) х =0:
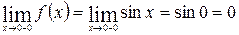 ;
; 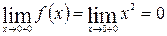 ;
; 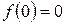 .
.
Так как предел функции при 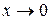 слева, равен пределу функции при
слева, равен пределу функции при 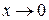 справа и равен значению функции при х =0, то в этой точке функция непрерывна.
справа и равен значению функции при х =0, то в этой точке функция непрерывна.
б) х =1:
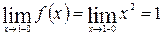 ;
; 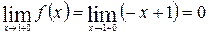 .
.
Так как предел слева не равен пределу справа, то в точке х =1 функция имеет разрыв 1-го рода, со скачком 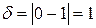 .
.
Дата публикования: 2014-10-20; Прочитано: 376 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!