 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Элементы аналитической геометрии
|
|
Пример. Даны координаты вершин пирамиды
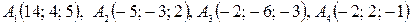 .
.
Найти:
1) длину ребра А 1 А 2;
2) угол между ребрами А 1 А 2 и А 1 А 4;
3) уравнения прямой А 1 А 2;
4) уравнение плоскости А 1 А 2 А 3;
1) Найдем координаты вектора 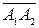 :
:
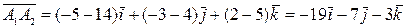 .
.
Длину вектора А 1 А 2 найдем по формуле:
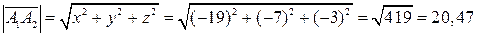 .
.
2) Вектор 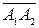 уже найден. Найдем вектор
уже найден. Найдем вектор 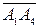 :
:
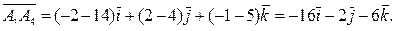
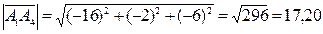 .
.
Скалярное произведение векторов 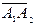 и
и 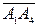 найдем по формуле:
найдем по формуле:
 .
.
Косинус угла 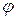 между векторами
между векторами 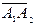 и
и 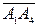 найдем по формуле:
найдем по формуле:
 ,
, 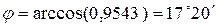 .
.
3) Составим уравнения прямой А 1 А 2, где 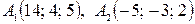 . Воспользуемся уравнениями прямой, проходящей через две точки
. Воспользуемся уравнениями прямой, проходящей через две точки 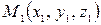 и
и 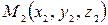 :
: 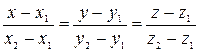 .
.
Принимая за точки 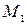 и
и 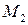 соответственно
соответственно 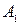 и
и 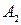 , получим:
, получим: 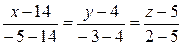 .
.
Таким образом, 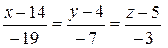 — уравнения прямой
— уравнения прямой 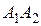 .
.
4) Составим уравнение плоскости 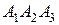 :
:
Пусть точка 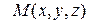 принадлежит плоскости
принадлежит плоскости 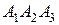 . Рассмотрим векторы
. Рассмотрим векторы 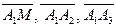 и найдем их координаты:
и найдем их координаты:
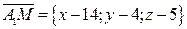 ,
, 
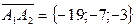 ,
, 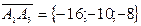 .
.
Так как данные вектора компланарны, то их смешанное произведение 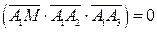 . Поэтому
. Поэтому
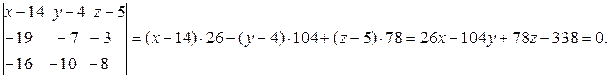
Сократив на (26), получим уравнение 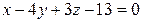 . Это и есть уравнение плоскости
. Это и есть уравнение плоскости 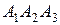 .
.
Пример. Даны вершины треугольника 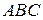 :
: 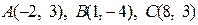 . Найти:
. Найти:
а) уравнения сторон треугольника;
б) систему неравенств, областью решений которой является множество точек, лежащих внутри и на границе треугольника.
Сделаем чертеж (рис.1)

|
а) Составим уравнения сторон треугольника 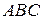 . Воспользуемся уравнением:
. Воспользуемся уравнением: 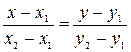 .
.
Так как точки  принадлежат прямой АС, то
принадлежат прямой АС, то
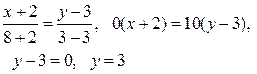
и 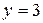 — уравнение прямой АС.
— уравнение прямой АС.
Так как точки 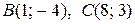 принадлежат прямой ВС, то
принадлежат прямой ВС, то
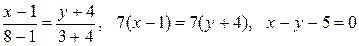 , и
, и
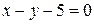 — уравнение прямой ВС.
— уравнение прямой ВС.
Аналогично найдем уравнение прямой АВ: 7 х +3 у +5=0
б) Рассмотрим уравнение 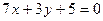 . Этому уравнению удовлетворяют точки, лежащие на прямой АВ. Начало координат, т.е. точка О (0,0) лежит внутри треугольника АВС и координаты точки О (0,0) удовлетворяют неравенству
. Этому уравнению удовлетворяют точки, лежащие на прямой АВ. Начало координат, т.е. точка О (0,0) лежит внутри треугольника АВС и координаты точки О (0,0) удовлетворяют неравенству  , так как
, так как 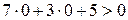 . Поэтому и координаты всех точек, лежащих с той же стороны от прямой АВ, что и точка О, будут удовлетворять неравенству
. Поэтому и координаты всех точек, лежащих с той же стороны от прямой АВ, что и точка О, будут удовлетворять неравенству  .
.
Уравнению 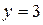 удовлетворяют точки, лежащие на прямой АС. Координаты точки О (0,0) удовлетворяют неравенству
удовлетворяют точки, лежащие на прямой АС. Координаты точки О (0,0) удовлетворяют неравенству 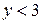 , так как 0<3. Следовательно и все точки, лежащие с той же стороны от прямой АС, что и точка О будут удовлетворять неравенству
, так как 0<3. Следовательно и все точки, лежащие с той же стороны от прямой АС, что и точка О будут удовлетворять неравенству 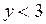 .
.
Уравнению 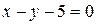 удовлетворяют координаты точек, лежащих на прямой ВС. Координаты точки О (0,0) удовлетворяют неравенству
удовлетворяют координаты точек, лежащих на прямой ВС. Координаты точки О (0,0) удовлетворяют неравенству 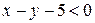 , так как
, так как 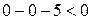 . Поэтому координаты всех точек, лежащих с той же стороны от прямой ВС, что и точка О (0,0), будут удовлетворять неравенству
. Поэтому координаты всех точек, лежащих с той же стороны от прямой ВС, что и точка О (0,0), будут удовлетворять неравенству 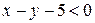 .
.
Таким образом, координаты точек, лежащих как внутри треугольника АВС, так и на его границах будут удовлетворять системе неравенств:
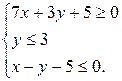
Дата публикования: 2014-10-20; Прочитано: 704 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
