Линии второго порядка

Если центр окружности, эллипса, гиперболы или вершина параболы находятся в точке ,то соответствующие уравнения этих кривых будут иметь вид:

— окружность;

— гипербола;

— эллипс;

или — параболы.

Пример. Привести к каноническому виду уравнение линии второго порядка и построить эту линию .

Преобразуем уравнение, выделяя полные квадраты с переменными и :

,

,

,

,

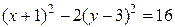— это уравнение гиперболы с центром в точке , действительная полуось а= 4, мнимая полуось (рис. 2).

Примеры решения заданий контрольной работы № 2