Дифференциальные уравнения второго порядка

Наиболее важными для практики являются линейные уравнения второго порядка.

Эти уравнения имеют вид

.

Общим решением этого уравнения будет

,

где — общее решение соответствующего уравнения без правой части (однородного): , а — некоторое частное решение исходного уравнения.

Будем рассматривать наиболее часто встречающиеся в практике случаи, когда коэффициенты являются постоянными числами, а правая часть имеет простой (специальный) вид. Для нахождения составляется характеристическое уравнение , находятся его корни и и, в зависимости от их значений, определяется .

Правило нахождения укажем в таблице № 1:

Характеристическое уравнение: Дискриминант:

1. — действительные и различные:

2. — действительные и равные:

3. — комплексно сопряженные:

Частное решение y^* находится по правилу, указанному в таблице №2:

f (x)	y*
f (x) =Pn (x)	1.y*=Qn (x), если среди корней характеристического уравнения нет числа 0. 2.y*=Qn (x)× x, если число 0 является однократным корнем характеристического уравнения. 3.y*=Qn (x)× x2, если число 0 является двукратным корнем характеристического уравнения.
f (x) =Pn (x) eax	4.y*=Qn (x)× eax, если среди корней характеристического уравнения нет числа a. 5.y*=Qn (x) eax × х, если a является однократным корнем характеристического уравнения. 6.y*=Qn(x) × eax × х2, если a является двукратным корнем характеристического уравнения.
f (x) =a0cosbx+b0sinbx	7.y*=Aсosbx+Bsinbx, если число bi, где 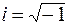- мнимая единица, не является корнем характеристического уравнения. 8.y*=(Acosbx+Bsinbx)х, если число bi является корнем характеристического уравнения.

В этой таблице Q_n (x)=A₀xⁿ+ A₁x^n-1+…+ A_n многочлен той же степени, что и P_n (x), но с неизвестными коэффициэнтами, которые и нужно найти.

Примеры.

1.Найти общее решение уравнения у^// – 5 у^/=х.

Обозначим искомое решение через у. Тогда у=`у+у<sup>*</sup>, где ` у — общее решение уравнения у^// – 5 у^/= 0. Составим характеристическое уравнение: k²- 5 k= 0; k (k- 5)=0; k₁= 0; k₂ =5. Следовательно `у=с ₁ е ^{0 х}+с ₂ е ^{5 х}=с ₁ +с ₂ е ^{5 х}. Найдем теперь у^*. Так как правая часть уравнения равна f (x) = 1× х+ 0, то частное решение у^* было бы: у^*=Ах+В, если бы числа 0 не было среди корней характеристического уравнения. Но в нашем случае 0 встречается среди корней характеристического уравнения один раз.Это случай 2, табл. № 2. Поэтому у^*=(Ах+В)х=Ах²+Вх. Найдем (у^*) ^/= 2 Ах+В; (у^*) ^/= 2 А, подставим эти значения в данное уравнение и потребуем, чтобы оно обратилось в тождество:

2 А- 5(2 Ах+В)º1× х+ 0; -10 Ах+ 2 А- 5 Вº 1× х+ 0, откуда

.

Таким образом, и общее решение уравнения будет

.

2. Найти общее решение уравнения у^//+ 4 у^/+ 13 у= 2cos4 x

Обозначим искомое решение через у. Тогда у=`у+у<sup>*</sup>, где ` у — общее решение уравнения у^//+ 4 у^/+ 13 у = 0. Составим характеристическое уравнение k²+4k+13= 0.Решая это уравнения находим корни: k₁=–2+3i; k₂=–2 – 3i. Следовательно `у=е ^{-2 х}(C ₁cos3x +C ₂ sin3x). Найдем теперь у^*. Т.к. b=4i нет среди корней характеристического уравнения (случай 7 табл.2), то частное решение у^* подбираем в виде у^*=Acos4x+Bsin4x; (у^*)^/=–4Asin4x+4Bcos4x; (у^*)^//=–16Acos4x–16Bsin4x. Подставляем эти значения в уравнение, приводим подобные слагаемые, получаем: cos4x(16B-3A)+sin4x(-16A-3B)=2cos4x. Приравниваякоэффициэнты при sin 4x и cos 4x находим:

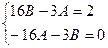
Решая систему получаем

Частное решение имеет вид

Общее решение уравнения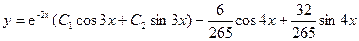

3. Найти частное решение уравнения у^//+ 4 у^/+ 4 у= 3 е ^{2 х} , удовлетворяющее начальным условиям у (0)=1, у ^/(0)=2.

Найдем сначала общее решение данного уравнения у=`у+у^*.

у^//+ 4 у^/+ 4 у=0; k ² + 4 k+ 4=0; D =16-16=0; Следовательно, `у=с <sub>1</sub> е <sup>-2 х</sup>+с <sub>2</sub> е <sup>-2 х</sup>х. Так как числа a= 2 нет среди корней характеристического уравнения (случай 4 табл. №2), то частное решение у<sup>*</sup> подбираем в таком же виде, как и правая часть у<sup>*</sup>=Ае <sup>2 х</sup> ; (у<sup>*</sup>)<sup>/</sup>=Ае <sup>2 х</sup> × 2; (у<sup>*</sup>)<sup>//</sup>=Ае <sup>2 х</sup>× 4. Подставляем эти значения в уравнение 4 Ае <sup>2 х</sup> + 4×2 Ае <sup>2 х</sup>+ 4 Ае <sup>2 х</sup>= 3 е <sup>2 х</sup>; 16 Ае <sup>2 х</sup> = 3 е <sup>2 х</sup> ; 16 А= 3; А= . Следовательно, у<sup>*</sup>= е <sup>2 х</sup> . Значит, у=`у+у^*= =с ₁ е ^{-2 х}+с ₂ е ^{-2 х}х+ 3/16 е ^{2 х} — общее решение данного уравнения. Для нахождения частного решения, удовлетворяющего заданным начальным условиям, найдем ещё

у^/=с ₁ е ^{-2 х} (-2) +с ₂(е ^{-2 х} (-2) х+е^{- 2 х}× 1)+3/16 е ^{2 х}× 2. Так как у (0)=1 и у ^/(0)=2, то получим .

Подставляя эти значения в общее решение, найдем окончательно . Это есть частное решение данного уравнения, удовлетворяющее данным начальным условиям.

Ряды

Рассмотрим бесконечную последовательность действительных чисел а ₁, а ₂, …, а_n,...

Выражение вида

а ₁+ а ₂+ а ₃+... а_n+... (2)

называется числовым рядом.

Рассмотрим S_n= а ₁+ а ₂+ а ₃+... а_n – n-ю частичную сумму ряда (2)

Если 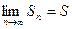,где S – действительное число, то это число называется суммой ряда (2),а сам этот ряд называется сходящимся. Если же S=∞ или не существует вообще, то ряд суммы не имеет и называется расходящимся.

Для рядов с положительными членами справедливы достаточные признаки сходимости.

Признак сравнения.

Пусть даны два ряда

а ₁+ а ₂+ а ₃+... а_n+... (3)

b ₁+ b ₂+ b ₃+... b_n+... (4)

причем a_n ≤ b_n (n= 1, 2, 3,...). Тогда из сходимости ряда (4) следует сходимость ряда (3). Из расходимости ряда (3) следует расходимость ряда (4).

Предельный признак сравнения: если существует конечный и отличный от нуля предел , то оба ряда (3) и (4) одновременно сходятся или одновременно расходятся.

Признак Даламбера.

Если для ряда (2) существует , то этот ряд сходится при l <1 и расходится при l >1.

Признак Коши.

Если для ряда (2) существует , то ряд сходится при l <1 и расходится при l >1.

Интегральный признак.

Если f (x) при х ≥1 непрерывная, положительная, монотонно убывающая функция, причем f (n) =a_n (n =1,2,...), то ряд (2) сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл .

Для знакочередующихся рядов вида

а ₁— а ₂ + а ₃ —...+...(-1) ⁿ⁺¹а_n+..., (5)

где a_n ≥0,справедлив признак Лейбница:

Если абсолютные величины членов ряда (5) монотонно убывают, а общий член ряда стремится к нулю, т.е., если выполняются условия:

1) а ₁> а ₂> а ₃>..> а_n >... и 2) ,

то ряд (5) сходится.

Можно доказать, что сумма сходящегося знакочередующегося ряда (5) не превосходит абсолютной величины первого члена этого ряда.