Образцы решений заданий контрольной работы № 3

Пример. Найти частные производные следующих функций:

1) ;

2) ;

3) .

1)Пусть .

Считая переменную константой, найдем

.

Считая константой переменную 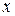, получим:

.

2)Пусть . Тогда

.

3)Пусть . Тогда

;

;

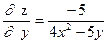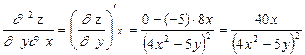
Убеждаемся, что

Пример. Дана функция , точка М ₀(2,-3) и вектор . Найти в точке М ₀ и производную по направлению вектора в этой же точке.

Имеем .

Находим

;

;

;

.

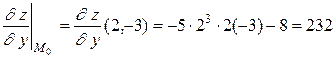Следовательно .

Далее, — производная по направлению вектора в точке М ₀.

Находим

Имеем: . Значит, Поэтому

Пример. Требуется изготовить закрытый цилиндрический бак данного объема V. Стоимость квадратного метра материала, идущего на изготовление стенки бака равна 8 рублей, а на изготовление дна и крышки – 6 руб. Определить размеры бака так, чтобы затраты на покупку материала, идущего на его изготовление, были наименьшими.

Решение. Площадь полной поверхности бака равна S=S_бок.+S_осн.=2p r×h+2p r². Объем бака равен V=p r²h, где r и h – радиус основания и высота бака соответственно. Стоимость материала, идущего на изготовление бака будет u (r, h) =2p rh×8+2p r²×6 (руб.). Нужно найти min этой функции, при условии, что pr²×h=V или pr²h-V=0. Составим функцию:

F (r, h) =2p rh×8+2pr²×6+l (p r²h-V)

Найдем ее производные по переменным r, h, l и приравняем их к нулю.

.

Из второго уравнения системы (при ) находим , откуда , тогда из первого уравнения получим или , т.е. . Подставляем это значение в третье уравнение ед. длины масштаба и тогда ед. длины масштаба.

Из экономического смысла задачи следует, что min функции u (r, h) существует, и будет определяться найденными значениями r и h. Очевидно также

или (руб.)

Пример. Экспериментально получены пять значений искомой функции при пяти значениях аргумента, которые записаны в таблице:

xi
yi	0,5		1,5

Методом наименьших квадратов найти искомую функциональную зависимость в виде . Экспериментальные точки и полученную прямую изобразить в системе координат XOY.

Запишем систему уравнений для нахождения коэффициентов k и b.

.

Учитывая, что n =5 и значения x_i и y_i известны, находим

;

;

;

Получаем

или , откуда .

Таким образом, наилучшее приближение к искомой зависимости в линейной форме имеет вид (см. рис.).