 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Дифференциальные уравнения. 1. Дифференциальные уравнения с разделяющимися переменными
|
|
1. Дифференциальные уравнения с разделяющимися переменными.
Эти уравнения можно представить в виде:
y/ = f1 (x) ×f2 (y) или P1 (x) Q1 (y) dx+P2 (x) Q2 (y) dy= 0.
Решения этих уравнений поясним на примерах.
Пусть y/=y cos x; тогда  , dy=y× сos x×dx;
, dy=y× сos x×dx;  . Интегрируя обе части полученного равенства, найдем ln
. Интегрируя обе части полученного равенства, найдем ln  = sin x+c, откуда y=e sin x+c — общее решение данного уравнения.
= sin x+c, откуда y=e sin x+c — общее решение данного уравнения.
Рассмотрим уравнение  .
.
Разделим обе части полученного уравнения на  .
.
Получим:  .
.
Переменные х и у разделились в этом равенстве. Интегрируя его, найдем:  .
.
Вычислим первый интеграл  :
:
Пусть  тогда
тогда  ,
, 
 .
.
Второй интеграл вычисляется аналогично:  .
.
Следовательно,
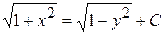 — это общий интеграл данного уравнения.
— это общий интеграл данного уравнения.
Выражая из общего интеграла функцию у, можно найти общее решение дифференциального уравнения.
2. Однородные дифференциальные уравнения первого порядка.
Уравнение первого порядка  называется однородным, если f (x, y) является однородной функцией нулевого порядка, т.е. f(tx,ty)=t0f(x,y)=f(x,y).
называется однородным, если f (x, y) является однородной функцией нулевого порядка, т.е. f(tx,ty)=t0f(x,y)=f(x,y).
Подстановкой  , или
, или 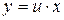 , это уравнение сводится к уравнению с разделяющимися переменными.
, это уравнение сводится к уравнению с разделяющимися переменными.
Пример. Найти общее решение уравнения 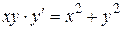 .
.
Находим  ,
,  . Делаем подстановку:
. Делаем подстановку:  . Тогда
. Тогда

Интегрируя, получим
 .
.
Следовательно  — общее решение данного уравнения.
— общее решение данного уравнения.
3. Линейные дифференциальные уравнения.
Уравнение вида:  где
где  непрерывные в некоторой области функции, называется линейным. Это уравнение сводится к уравнению с разделяющимися переменными подстановкой
непрерывные в некоторой области функции, называется линейным. Это уравнение сводится к уравнению с разделяющимися переменными подстановкой  , действие которой покажем на примере.
, действие которой покажем на примере.
Пример. Найти общее решение уравнения  .
.
Делаем подстановку  , где u и v неизвестные пока функции аргумента х. Находим
, где u и v неизвестные пока функции аргумента х. Находим  и подставляем значения
и подставляем значения  и
и  в данное уравнение
в данное уравнение 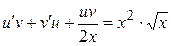 или
или  . Выберем функцию
. Выберем функцию  так, чтобы
так, чтобы  . Тогда функция
. Тогда функция  будет находиться из уравнения
будет находиться из уравнения  . Таким образом, нахождение неизвестной функции
. Таким образом, нахождение неизвестной функции  сводится к последовательному нахождению функций
сводится к последовательному нахождению функций  и
и  из указанных уравнений:
из указанных уравнений:

Подставим это значение в уравнение  . Получим
. Получим  или
или  Интегрируя это равенство найдем
Интегрируя это равенство найдем  и окончательно,
и окончательно,  — общее решение данного уравнения.
— общее решение данного уравнения.
Дата публикования: 2014-10-20; Прочитано: 337 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
