 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Неприводимые многочлены над
|
|
Теорема 18.2. (Критерий Эйзенштейна). Если для многочлена 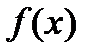 с целыми коэффициентами (
с целыми коэффициентами (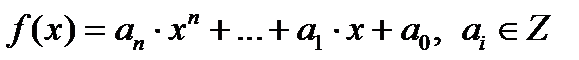 ) такими, что
) такими, что 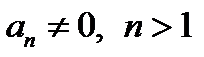 существует простое число
существует простое число 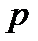 с условиями: 1)
с условиями: 1) 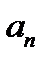 не делится на
не делится на 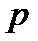 ; 2)
; 2) 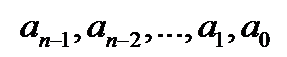 ⋮
⋮ 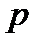 и 3)
и 3) 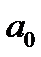 не делится на
не делится на  , то
, то 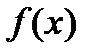 неприводим над полем рациональных чисел
неприводим над полем рациональных чисел 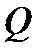 .
.
Замечание. Критерий Эйзенштейна не является критерием в полном смысле этого слова, так как теорема обратной силы не имеет.
Следствие. Над полем рациональных чисел 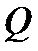 существуют неприводимые многочлены любой степени
существуют неприводимые многочлены любой степени 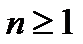 .
.
В качестве примеров таких многочленов можно взять многочлены вида 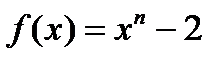 , которые удовлетворяют всем требованиям критерия Эйзенштейна (
, которые удовлетворяют всем требованиям критерия Эйзенштейна (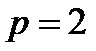 ).
).
Заметим, что критерий Эйзенштейна применим не ко всем неприводимым над полем 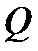 многочленам. В некоторых случаях помогает
многочленам. В некоторых случаях помогает
Теорема 19.2. Если 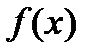 многочлен с рациональными коэффициентами и
многочлен с рациональными коэффициентами и 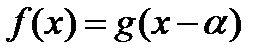 , где
, где 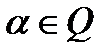 , то
, то 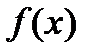 неприводим над
неприводим над 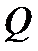 тогда и только тогда, когда многочлен
тогда и только тогда, когда многочлен 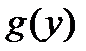 неприводим над
неприводим над 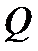 .
.
Пример 20. 1) К многочлену 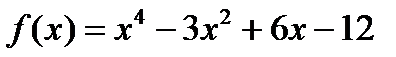 критерий Эйзенштейна применим напрямую (достаточно взять
критерий Эйзенштейна применим напрямую (достаточно взять 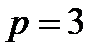 ). Значит,
). Значит, 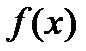 неприводим.
неприводим.
2) Пусть 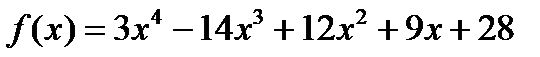 . К этому многочлену критерий Эйзенштейна напрямую применить невозможно. Разложим
. К этому многочлену критерий Эйзенштейна напрямую применить невозможно. Разложим 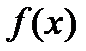 по степеням
по степеням 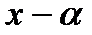 , подбирая многочлен
, подбирая многочлен 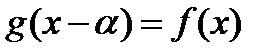 , к которому можно применить критерий Эйзенштейна. Вообще говоря, нужно последовательно перебирать значения
, к которому можно применить критерий Эйзенштейна. Вообще говоря, нужно последовательно перебирать значения  , пока не натолкнёмся на подходящее. Мы же сразу возьмём
, пока не натолкнёмся на подходящее. Мы же сразу возьмём 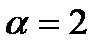 и разложим
и разложим 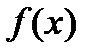 по степеням
по степеням 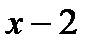 с применением алгоритма, следующего из схемы Горнера.
с применением алгоритма, следующего из схемы Горнера.
| -14 | |||||
| -8 | -4 | ||||
| -2 | -8 | -15 | |||
Таким образом, 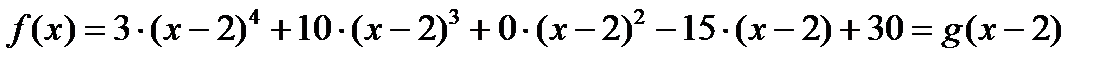 , где
, где 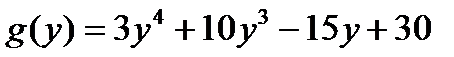 неприводим над полем
неприводим над полем 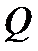 (достаточно для применения критерия Эйзенштейна взять
(достаточно для применения критерия Эйзенштейна взять 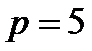 ). Значит, по теореме 19.2 и многочлен
). Значит, по теореме 19.2 и многочлен 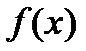 неприводим над полем
неприводим над полем 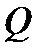 .
.
9. Нахождение рациональных корней многочленов с рациональными коэффициентами.
Нахождение рациональных корней многочлена 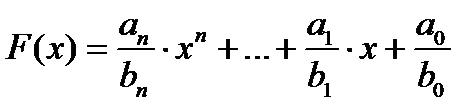 с рациональными коэффициентами (
с рациональными коэффициентами (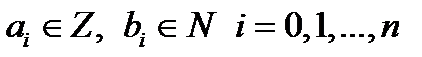 ) сводится к задаче о нахождении рациональных корней многочлена с целыми коэффициентами, так как
) сводится к задаче о нахождении рациональных корней многочлена с целыми коэффициентами, так как 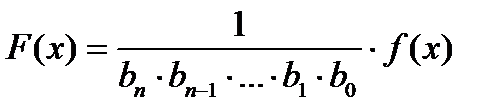 , где
, где 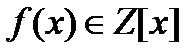 и любой корень многочлена
и любой корень многочлена 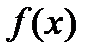 является корнем многочлена
является корнем многочлена 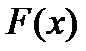 и наоборот.
и наоборот.
Дата публикования: 2014-10-20; Прочитано: 3713 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
