 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Деление с остатком в . Схема Горнера
|
|
Определение. Разделить с остатком многочлен  на ненулевой многочлен
на ненулевой многочлен 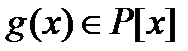 - значит найти многочлены
- значит найти многочлены 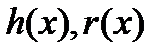
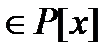 такие, что
такие, что
1) 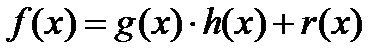 и 2)
и 2) 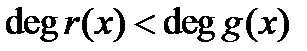 .
.
При этом многочлен 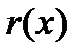 называется остатком, а
называется остатком, а 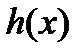 - неполным частным.
- неполным частным.
Теорема 8.2. (О делении многочленов с остатком в 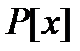 ). Для любых многочленов
). Для любых многочленов 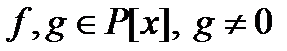 существуют, причём единственные многочлены
существуют, причём единственные многочлены 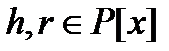 такие, что 1)
такие, что 1) 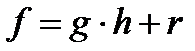 и 2)
и 2) 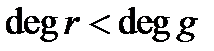 .
.
Таким образом, деление с остатком любого многочлена на ненулевой многочлен с коэффициентами из одного и того же поля всегда возможно, причём единственным образом.
Деление с остатком многочленов производится, как и для натуральных чисел, уголком, начиная с верхнего правого угла.
Схема Горнера – это алгоритм деления с остатком многочлена 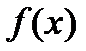 на
на 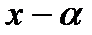 .
.
Если 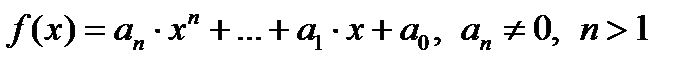 , то по теореме Безу существует единственный многочлен
, то по теореме Безу существует единственный многочлен 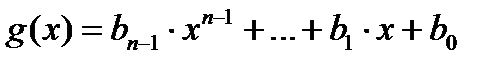 такой, что
такой, что 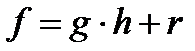 . Тогда
. Тогда
получаем следующую систему соотношений:
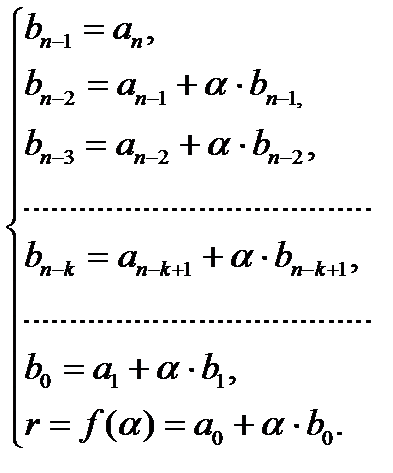
Замечаем следующую зависимость: 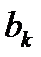 получается как сумма
получается как сумма 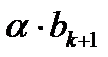 и
и 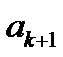 . Заготовкой для вычислений является таблица:
. Заготовкой для вычислений является таблица:
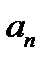
| 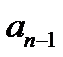
| 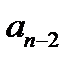
| …. | 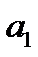
| 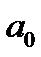
| |
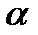
| 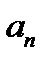
|
Для того, чтобы заполнить первую слева незаполненную клеточку во второй строке, нужно 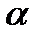 умножить на элемент, стоящий в предыдущей клеточке второй строки, и результат сложить с элементом, стоящим над вычисляемой клеточкой в первой строке.
умножить на элемент, стоящий в предыдущей клеточке второй строки, и результат сложить с элементом, стоящим над вычисляемой клеточкой в первой строке.
Все дальнейшие вычисления производим в таблице:
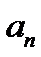
| 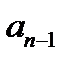
| 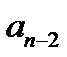
| …. | 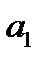
| 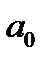
| |
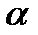
| 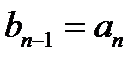
| 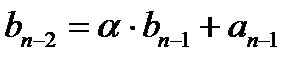
| 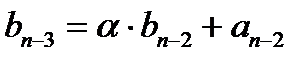
| …. | 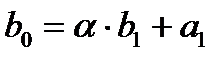
| 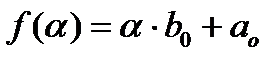
|
Пример 17. Разделить с остатком 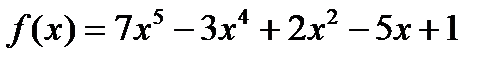 на
на 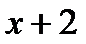 .
.
В данном случае 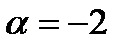 . Заполняем заготовку:
. Заполняем заготовку:
| -3 | -5 | |||||
| -2 |
Далее производим вычисления:
| -3 | -5 | |||||
| -2 | -17 | -66 | -253 |
Значит, 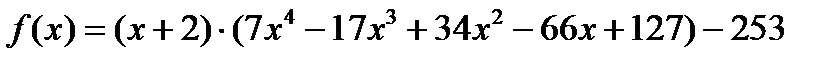 .
.
В частности, 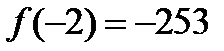 .
.
Схема Горнера применяется во многих случаях. В частности, при определении кратности корня многочлена.
Определение. Пусть 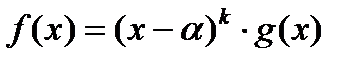 , где
, где 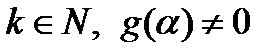 . Тогда
. Тогда 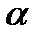 называется корнем кратности
называется корнем кратности 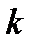 многочлена
многочлена 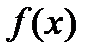 . Если
. Если 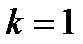 , то
, то 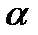 называется простым корнем.
называется простым корнем.
Пример 18. Найти кратность корня 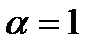 многочлена
многочлена 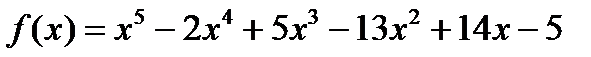 .
.
По теореме Безу кратность корня 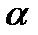 равна количеству делений
равна количеству делений 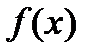 на
на 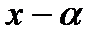 с нулевым остатком. Все вычисления выполняем в одной таблице:
с нулевым остатком. Все вычисления выполняем в одной таблице:
| -2 | -13 | -5 | ||||
| -1 | -9 | |||||
| -5 | ||||||
7 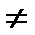 0 0
|
Значит, 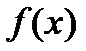 ⋮
⋮ 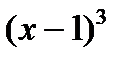 , но не делится на
, но не делится на 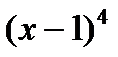 . Поэтому кратность корня
. Поэтому кратность корня 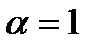 многочлена
многочлена 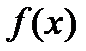 равна 3.
равна 3.
Заметим, что при вычислении значений в третьей и т.д. строках таблицы, требуемые по схеме Горнера числа брали из стоящей выше строки.
Дата публикования: 2014-10-20; Прочитано: 947 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
