Наибольший общий делитель. Взаимная простота и неприводимость

Определение. Многочлен называется общим делителем (ОД) многочленов , если каждый из этих многочленов делится на D.

Многочлен d называется наибольшим общим делителем многочленов , если 1) d - ОД этих многочленов; 2) d делится на любой ОД многочленов .

Обозначение. Нормированным НОД многочленов называется такой НОД, старший коэффициент которого равен 1. Обозначим его через (, ).

Теорема 9.2 (Об определяющих свойствах НОД).

1)Если НОД двух многочленов существует, то он определён с точностью до ассоциированности.

2)Есл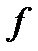и ⋮ и нормирован, то(, )= .

3)Если , где - многочлены из и , то .

4)Если хотя бы один из многочленов не равен 0, то их НОД существует.

Алгоритм Евклида или метод последовательного деления с остатком применим и в .Но в случае многочленов модуль (норма в ) заменяется на степень (норма в ). Пусть и – ненулевые многочлены. Делим на с остатком r₁. Если r₁≠0, то делим с остатком r₂ на r₁. Если r₂≠0, то делим r₁ на r₂ с остатком r₃ и т.д. до тех пор, пока очередной остаток r_n+1 не станет равным нулю:

, где , r₁ – многочлены из и ,

, где 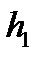, r₂ - – многочлены из и ,

………………

r_n-2=r_n-1∙ _n-1+r_n, где _n-1, r_n - – многочлены из и ,

r_n-1=r_n∙ 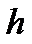_n+0, где 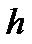_n – многочлен из .

Теорема 10.2. Последний ненулевой остаток в алгоритме Евклида для ненулевых многочленов равен их наибольшему делителю.

Следствие. Для любых ненулевых многочленов из существуют такие, что (линейное выражение наибольшего общего делителя двух ненулевых многочленов из ).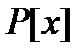

Определение. Многочлены называются взаимно простыми, если 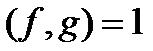, т.е. общими делителями этих многочленов могут быть только ненулевые элементы поля .

Теорема 11.2. (Основные свойства взаимной простоты).

1) Многочлены взаимно просты тогда и только тогда, когда существуют многочлены такие, что .

2) Если многочлены взаимно простые и ⋮ , то ⋮ для любого многочлена .

Определения. Многочлен степени большей или равной 1 называется приводимым над полем , если существуют многочлены такие, что

1) и 2) .

Многочлен степени большей или равной 1 называется неприводимым над полем , если его нельзя представить в виде , где 1) и

2) .

Пример 19. 1) Многочлен приводим над полями . 2) Многочлен приводим над полями , но неприводим над полем . 3) Многочлен приводим над полем 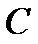, но неприводим над полями .

Замечания. 1) Многочлены, являющиеся элементами поля (т.е. многочлены нулевой степени и нулевой многочлен), не являются ни приводимыми, ни неприводимыми. 2) Многочлен первой степени неприводим над любым полем, содержащим его коэффициенты. 3) Многочлен второй степени из приводим над полем тогда и только тогда, когда его корни лежат в поле . 4) Многочлен третьей степени из приводим над полем тогда и только тогда, когда хотя бы один его корень лежит в поле .

Теорема 12. 2. (Свойства неприводимости).

1) Если , 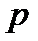неприводим над и ⋮ 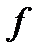, то либо , либо .

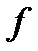2) Если , и - неприводим над полем , то либо ⋮ , либо .

3) Если взаимно прост с многочленами , то он взаимно прост и с их произведением .

4) Если ⋮ и неприводим, то либо ⋮ 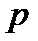, либо ⋮ .

5) Если ⋮ , где неприводимые и неассоциированные между собой, то ⋮ , т.е. и на их произведение.

Теорема 13.2. Всякий многочлен степени больше или равной 1 либо неприводим над , либо разлагается в произведение неприводимых над многочленов, причём это разложение единственно с точностью до ассоциированности и порядка следования сомножителей.