 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Многочлены над полем действительных чисел
|
|
Напомним, что если комплексное число имеет вид 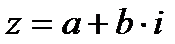 , то сопряжённое имеет вид
, то сопряжённое имеет вид 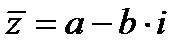 . При этом выполняются следующие свойства:
. При этом выполняются следующие свойства: 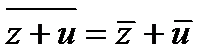 ;
; 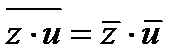 ;
; 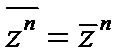 ;
; 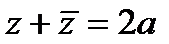 ;
; 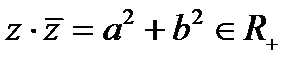 .
.
Теорема 16.2. (О комплексных корнях многочлена с действительными коэффициентами). 1) Если 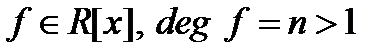 и
и 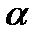 - корень
- корень 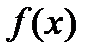 , то
, то 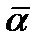 тоже корень
тоже корень 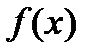 , т.е.
, т.е. 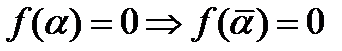 . 2) Если
. 2) Если 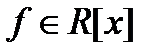 , то
, то 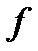 имеет чётное количество комплексных недействительных корней.
имеет чётное количество комплексных недействительных корней.
Следствие. Любой многочлен нечётной степени с действительными коэффициентами имеет хотя бы один действительный корень, а значит, приводим над полем 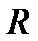 действительных чисел.
действительных чисел.
Теорема 17.2. (О неприводимых многочленах над полем 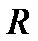 ). Над полем действительных чисел
). Над полем действительных чисел 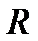 неприводимы только многочлены первой степени или многочлены
неприводимы только многочлены первой степени или многочлены 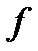 второй степени, для которых существуют
второй степени, для которых существуют 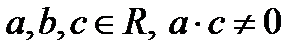 и такие, что
и такие, что 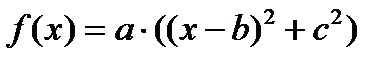 .
.
Следствие. Легко получить, что многочлен второй степени с действительными коэффициентами неприводим над полем действительных чисел 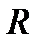 тогда и только тогда, когда его дискриминант отрицателен (
тогда и только тогда, когда его дискриминант отрицателен (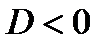 ).
).
Дата публикования: 2014-10-20; Прочитано: 3138 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
