 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Многочлены над полем комплексных чисел
|
|
Теорема 14. 2. (Основная теорема алгебры многочленов). Всякий многочлен  имеет корень в поле
имеет корень в поле 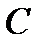 .
.
Следствия. 1) Многочлен 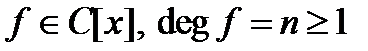 имеет в
имеет в 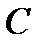 ровно
ровно  корней с учётом их кратности. 2) Над полем
корней с учётом их кратности. 2) Над полем 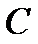 неприводимы только многочлены первой степени. 3) Если
неприводимы только многочлены первой степени. 3) Если 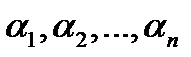 все корни многочлена
все корни многочлена 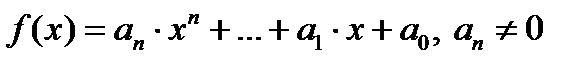 , то
, то 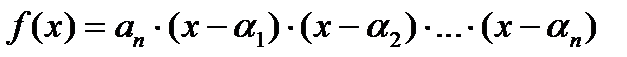 .
.
Теорема 15.2. (Формулы Виета). Пусть 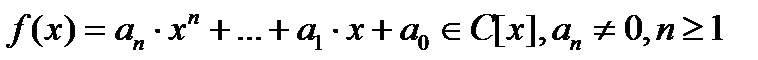 и
и  - все его корни с учётом их кратности. Тогда справедливы равенства:
- все его корни с учётом их кратности. Тогда справедливы равенства: 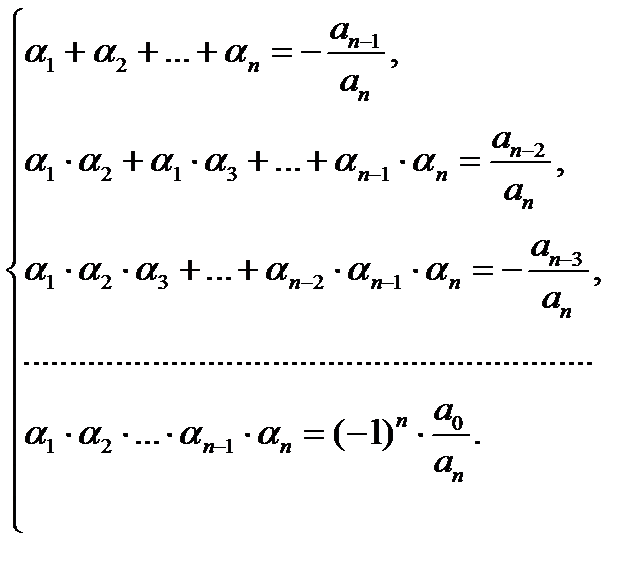
Дата публикования: 2014-10-20; Прочитано: 2247 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
