 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритм нахождения рациональных корней многочлена
|
|
1. Редукция от 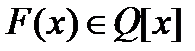 к
к 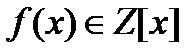 .
.
2. Находим 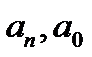 многочлена
многочлена 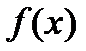 и все
и все 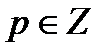 и
и 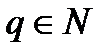 такие, что 1)
такие, что 1) 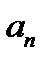 ⋮
⋮ 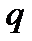 , 2)
, 2) 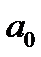 ⋮
⋮ 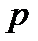 . Исключаем среди дробей
. Исключаем среди дробей 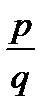 сократимые.
сократимые.
3. Находим 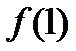 и
и 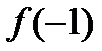 и проверяем выполнение условий
и проверяем выполнение условий 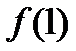 ⋮
⋮ 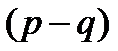
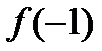 ⋮(
⋮(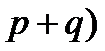 .
.
4. Для некоторых целых чисел 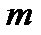 находим значения
находим значения 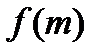 и проверяем выполнение условия
и проверяем выполнение условия 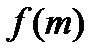 ⋮
⋮ 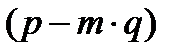 (пункты 3 и 4 нужны для отсеивания лишних претендентов на роль рациональных корней многочлена
(пункты 3 и 4 нужны для отсеивания лишних претендентов на роль рациональных корней многочлена 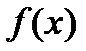 ).
).
5. Оставшиеся не отсеянными на роль корней дроби проверяем на выполнение условия 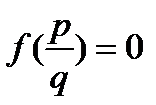 . Полученные корни и являются искомыми.
. Полученные корни и являются искомыми.
Пример 21. Найти рациональные корни многочлена 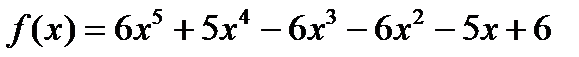 .
.
Данный многочлен имеет целые коэффициенты. Имеем 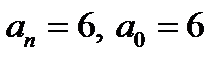 . Так как необходимо
. Так как необходимо 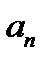 ⋮
⋮ 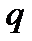 ,
, 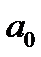 ⋮
⋮ 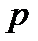 , то 6⋮
, то 6⋮  и 6⋮
и 6⋮  . Значит,
. Значит, 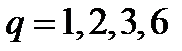 и
и 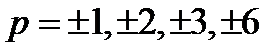 . Поэтому
. Поэтому 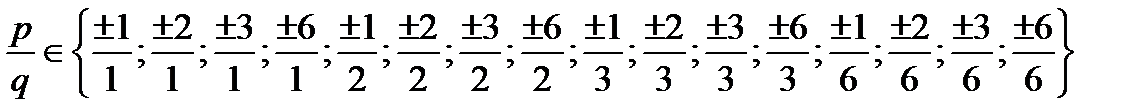 .
.
В этом множестве есть сократимые, т.е. не взаимно простые дроби. При решении их нужно исключить. Решение оформляем в виде таблицы, в клеточках которой, соответствующих дроби 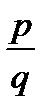 , ставим 0, если дробь является корнем
, ставим 0, если дробь является корнем  , и
, и  в противном случае. В нашей заготовке сразу исключим из рассмотрения сократимые дроби.
в противном случае. В нашей заготовке сразу исключим из рассмотрения сократимые дроби.
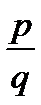
| -1 | -2 | -3 | -6 | ||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | - | - | - |
Теперь только дроби, соответствующие незаполненным клеточкам в таблице и только они, могут быть рациональными корнями многочлена 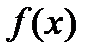 .
.
Вычисляем 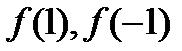 по схеме Горнера.
по схеме Горнера.
| -6 | -6 | -5 | ||||
| -1 | -6 | |||||
| -1 | -1 | -5 | -1 | -4 |
Значит, 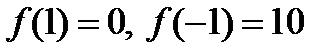 . 1 – корень
. 1 – корень 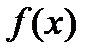 , -1 не является корнем. Поэтому можно проверять лишь выполнение условия
, -1 не является корнем. Поэтому можно проверять лишь выполнение условия 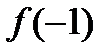 ⋮
⋮ 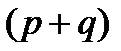 или 10⋮
или 10⋮ 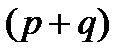 .
.
Заметим, что дробь 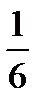 не является корнем
не является корнем 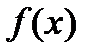 , так как для неё
, так как для неё 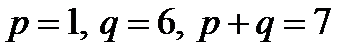 и 10 не делится на 7. Аналогично исключаем дроби:
и 10 не делится на 7. Аналогично исключаем дроби: 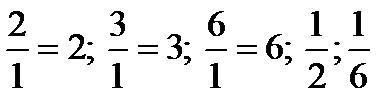 .
.
Далее находим 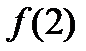 :
:
| -6 | -6 | -5 | ||||
Итак, 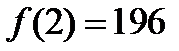 и, используя свойство
и, используя свойство 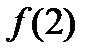 ⋮
⋮ 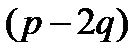 , исключаем дополнительно дроби:
, исключаем дополнительно дроби: 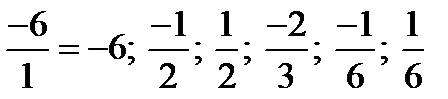 .
.
Оставшиеся дроби 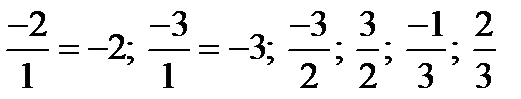 проверяем по схеме Горнера.
проверяем по схеме Горнера.
| -6 | -6 | -5 | ||||
| -2 | -7 | -22 | -39 | ≠0 | ||
| -3 | -13 | -105 | ≠0 | |||
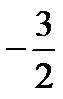
| -4 | -6 | ||||

| 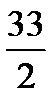
| ≠0 | ||||
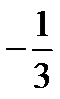
| -7 | ≠0 | ||||
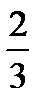
| -6 | -9 |
Итак, рациональными корнями данного многочлена 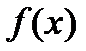 являются числа 1;
являются числа 1; 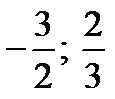 .
.
Дата публикования: 2014-10-20; Прочитано: 1510 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
