 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение квадратных уравнений. Теорема Виета
|
|
Теорема 1.2. Уравнение 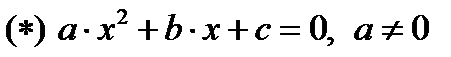 ,
, 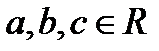 и
и 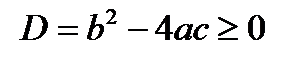 имеет два действительных корня, которые находятся по формулам
имеет два действительных корня, которые находятся по формулам  .
.
Теорема 2.2 (Теорема Виета). Если 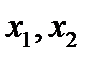 - корни уравнения (∗), то
- корни уравнения (∗), то 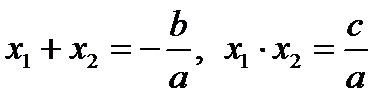 .
.
Следствие. Корни приведённого квадратного уравнения 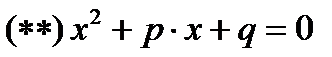 при условии
при условии 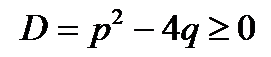 находятся по формулам
находятся по формулам 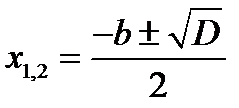 и теорема Виета для корней этого уравнения:
и теорема Виета для корней этого уравнения: 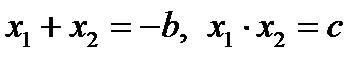 .
.
Теорема 3.2. (Обратная теорема Виета). Если 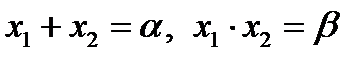 , то
, то 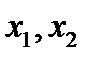 - корни квадратного уравнения
- корни квадратного уравнения 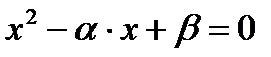 .
.
Следствие. Если 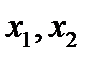 - корни уравнения
- корни уравнения 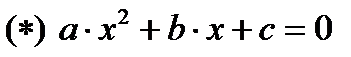 , то
, то 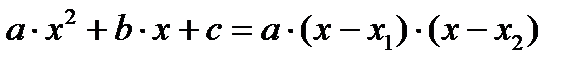 .
.
Пример 14. 1) Найдите приведённое квадратное уравнение с корнями 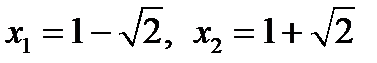 .
.
Так как 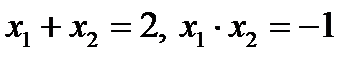 , то по теореме, обратной теореме Виета,
, то по теореме, обратной теореме Виета, 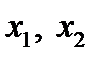 - корни приведённого квадратного уравнения
- корни приведённого квадратного уравнения 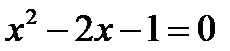 .
.
2) При каких значениях параметра 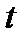 оба корня уравнения
оба корня уравнения 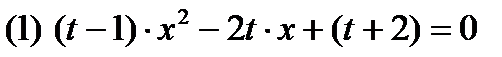 положительны?
положительны?
Для существования действительных корней уравнения требуется выполнение условия  . Итак,
. Итак, 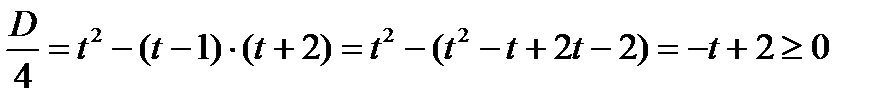 .
.
Числа 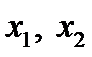 одного знака, если
одного знака, если 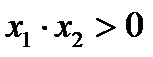 , а оба положительны, если
, а оба положительны, если 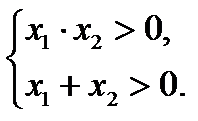
Но по теореме Виета 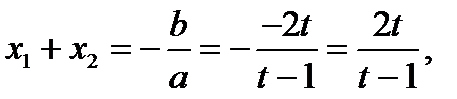
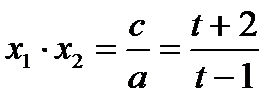 . Поэтому оба корня уравнения (1) положительны, если
. Поэтому оба корня уравнения (1) положительны, если
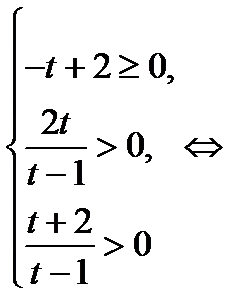
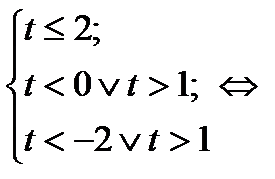

Дата публикования: 2014-10-20; Прочитано: 654 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
