Метод неопределенных коэффициентов для численного дифференцирования

В основном используется для случая произвольного расположения интерполяционных узлов. В данном случае искомое выражение k -ой производной в некоторой точке x = x _i представляется в виде линейной комбинации заданных значений функции y _j= f (x _j), в узлах

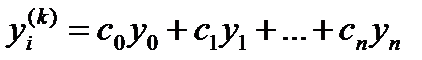(13)

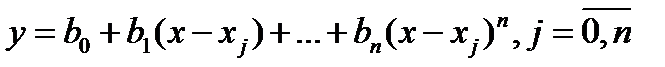Предполагается, что это соотношение выполняется точно, если y = f (x) является многочленом степени не выше n, т.е. если она может быть представлена в виде:

Отсюда следует, что соотношение (13) должно выполняться точно для многочленов y =1, y = x – x _j, y =(x – x _j)², y =(x – x _j) ⁿ.

Производные от них соответственно равны:

y ' = 0; y ' = 1; y ' = 2(x – x _j), y ' = n (x – x _j) ^{n –1}

Подставляя эти выражения в левую и правую части (13), получают систему линейных алгебраических уравнений (n + 1)-го порядка для вычисления значений c ₀, c ₁, …, c _n.

47.Метод прямоугольников:

Пусть рассматривается интервал [– h /2, h /2], где h > 0.

Предположим, что подынтегральная функция f (x) дважды непрерывно дифференцируема, т.е. f (x) Î C ²[ –h /2, h /2].

Тогда соотношение

запишется в виде: (10)

здесь взят один узел x = 0 и соответствующий вес q = h.

Полученная квадратурная формула

I = h*f (0) (11)

называется формулой прямоугольников для одного шага или формулой средних. Такое название определено, так как это есть площадь прямоугольника с высотой f (0) и основанием h. Из рисунка видно, что, уменьшая интервал h при гладкой функции f (x) (т.к. f (x) Î C ²[ –h /2, h /2]), погрешность R ® 0 при h ® 0. Доказано, что точность результата для (10) оценивается формулой

, где x Î [ –h /2, h /2].

Заметим, что квадратурная формула (11) является точной для полиномов первой степени,, так как

Иногда на интервале [ –h /2, h /2] применяют формулы вида I = h*f (– h /2) и I = h*f (h /2) – формулы правых и левых прямоугольников. Они точны только для полиномов нулевой степени, т.е. констант.

48.Метод трапеций:

Рассмотрим интервал [0, h ], h > 0

Предположим, что f (x) Î C ²[0, h ]. Соотношение запишем в виде:

(12)

где взяты два узла x₀ = 0, x₁ = h и соответствующие веса q ₀ = q ₁ = h /2.

Получаемая квадратурная формула

(13)

называется формулой трапеций для одного шага. Название связано с тем, что (13) при положительных значениях f (0), f (h) является площадью трапеции с основаниями f (0), f (h) и высотой h.

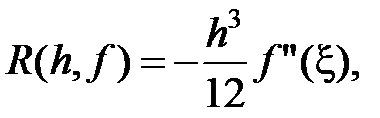Доказано, что погрешность для (12)

(14)

где x – некоторая точка интервала [ 0, h ]. Заметим, что (13) так же, как формула прямоугольников точна для полиномов первой степени.

49.Метод Симпсона:

Рассмотрим интервал [ –h, h ], h > 0. Предположим, что

f (x) Î C ⁴[– h, h ].

Для соотношения возьмем три узла x₀ = x_{i –1} = – h, x₁ = x_i =0,

x₂ = x_{i +1}= h. Соответствующие им весовые коэффициенты получим из аппроксимации f (x) параболой, построенной на точках

(– h, f (– h)), (0, f (0)), (h, f (h)) в виде квадратного многочлена

y = ax ² + bx + c.

Для получения коэффициентов a, b и c

построим многочлен Лагранжа второй степени,

проходящий через выбранные точки:

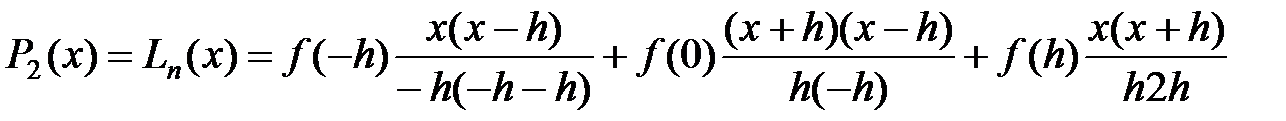
Вычисляем интеграл:

(16)

Тогда соотношение запишется в виде:

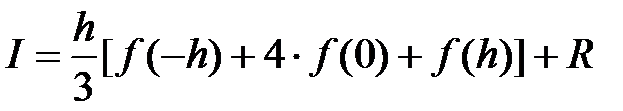(17)

и называется формулой Симпсона (парабол).

Доказано, что погрешность для формулы Симпсона оценивается соотношением:

(18)

где xÎ [– h, h ].

Из соотношения (18) следует, что квадратурная формула Симпсона точна для полиномов третьей степени.

Отметим, что при применении простейших квадратурных формул требуются вычисления значения подынтегральных функций f (x):

а) в одной точке – для формулы прямоугольников;

б) в двух точках – для формулы трапеций;

в) в трех точках – для формулы Симпсона.

50.Выбор шага интегрирования (пример):

Данная задача состоит в выборе шага h, обеспечивающего заданную точность e вычисления интеграла по выбранной формуле численного интегрирования.

Известны два подхода к решению данной задачи:

1) выбор шага по теоретическим оценкам погрешностей (23);

2) по косвенным схемам (эмпирическим оценкам).