 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Условия сходимости метода простой итерации для нелинейных систем уравнений второго порядка
|
|
Рассмотрим систему из двух уравнений общего вида

(3)
Нужно найти действительные корни x и y с заданной степенью точности e.
 Предположим, что данная система имеет корни и их можно установить. Итак, для применения метода простой итерации систему (3) нужно привести к виду:
Предположим, что данная система имеет корни и их можно установить. Итак, для применения метода простой итерации систему (3) нужно привести к виду:
(4)
где j1 и j2 – итерирующие функции. По ним и строится итерационный процесс решения в виде:

n = 0,1,2,… (5)
где при n = 0, x 0 и y 0 – начальные приближения.
Имеет место утверждение: пусть в некоторой замкнутой области R (a £ x £A; b £ y £B) имеется одно и только одно единственное решение x =g; y =b, тогда:
1) если j1(x, y) и j2(x, y) определены и непрерывно дифференцируемы в R;
2) если начальное решение x 0, y 0 и все последующие решения xn, yn также принадлежат R;
 3) если в R выполняются неравенства:
3) если в R выполняются неравенства:
(6)
 или равносильные неравенства:
или равносильные неравенства:
(6’)
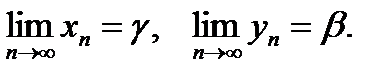
то тогда итерационный процесс (5) сходится к определенным решениям, т.е.
Оценка погрешности n -го приближения дается неравенством:

где М – наибольшее из чисел q 1 или q 2 в соотношениях (6) и (6`).
Сходимость считается хорошей, если М <1/2. Если совпадают три значащие цифры после запятой в соседних приближениях, то обеспечивается точность e = 10–3.
41.Метод Ньютона для систем решения нелинейных уравнений:
Для 2-х систем уравнений.
 Пусть дана система
Пусть дана система
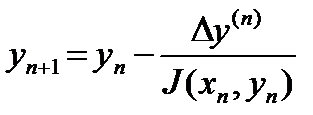
 Согласно методу Ньютона последовательные приближения типа (5) вычисляются по формулам
Согласно методу Ньютона последовательные приближения типа (5) вычисляются по формулам

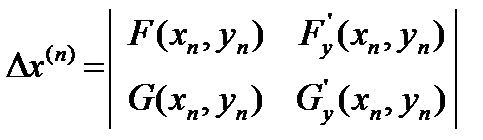 где
где
n = 0,1,2,...
и, если Якобиан
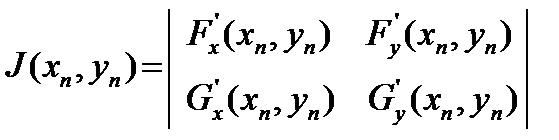
¹ 0
решение будет единственным.
Начальные значения x 0 и y0 определяются грубо (приближенно – графически или «прикидкой»). Данный метод эффективен только при достаточной близости начального приближения к истинному решению системы.
Для систем n-го порядка с n неизвестными
Для метода Ньютона функции Fi = (x 1, x 2,..., xn) из (1) раскладываются в ряд Тэйлора с отбрасыванием производных второго и выше порядков.
Пусть известен результат предварительной итерации при решении (1) дает результат для = (a 1, a 2,..., an).
Задача сводится к нахождению поправок этого решения: D x 1, D x 2,..., D xn.
Тогда при очередной итерации решение будет:
x 1 = a 1 + D x 1; x 2 = a 2 + D x 2; …, xn = an + D xn . (8)
Для нахождения D xi разложим Fi (x 1, x 2,..., xn) в ряд Тейлора:

(9)
 Приравняем правые части согласно (1) к нулю и получим систему линейных уравнений относительно D xi:
Приравняем правые части согласно (1) к нулю и получим систему линейных уравнений относительно D xi:
(10)
Значения F 1, F 2, …, Fn и их производных вычисляются при x 1= a 1, x 2= a 2,..., xn = an. Расчет ведется с учетом (8) по (9) и (10). Процесс прекращается, когда max|D xi | < e. При этом будет иметь место единственное решение системы, если Якобиан

По сходимости этот метод выше метода простой итерации.
Дата публикования: 2014-10-20; Прочитано: 1751 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
