Понятие адаптивных алгоритмов численного интегрирования

Из анализа погрешностей методов численного интегрирования следует, что точность получаемых результатов зависит как от характера изменения подынтегральной функции, так и от шага интегрирования. Будем считать, что величину шага мы задаем. При этом ясно, что для достижения сравнимой точности при интегрировании слабо меняющейся функции шаг можно выбирать большим, чем при интегрировании резко меняющихся функций.

На практике нередко встречаются случаи, когда подынтегральная функция меняется по-разному на отдельных участках отрезка интегрирования. Это обстоятельство требует такой организации экономичных численных алгоритмов, при которой они автоматически приспосабливались бы к характеру изменения функции. Такие алгоритмы называются адаптивными (приспосабливающимися). Они позволяют вводить разные значения шага интегрирования на отдельных участках отрезка интегрирования. Это дает возможность уменьшить машинное время без потери точности результатов расчета. Подчеркнем, что этот подход используется обычно при задании подынтегральной функции y=f(x) в виде формулы, а не в табличном виде.

Рассмотрим принцип работы адаптивного алгоритма. Первоначально отрезок [a,b] разбиваем на n частей. В дальнейшем каждый такой элементарный отрезок делим последовательно пополам. Окончательное число шагов, их расположение и размеры зависят от подынтегральной функции и допустимой погрешности e.

К каждому элементарному отрезку [xi-1, xi] применяем формулы численного интегрирования при двух различных его разбиениях. Получаем приближения для интеграла по этому отрезку:

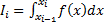(16)

Полученные значения сравниваем и проводим оценку их погрешности. Если погрешность находится в допустимых границах, то одно из этих приближений принимается за значение интеграла по этому элементарному отрезку. В противном случае происходит дальнейшее деление отрезка и вычисление новых приближений. С целью экономии времени точки деления располагаются таким образом, чтобы использовались вычисленные значения в точках предыдущего разбиения.

Процесс деления отрезка пополам и вычисления уточненных значений продолжается до тех пор, пока их разность станет не больше некоторой заданной величины , зависящей от e и h:

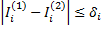(17)

Аналогичная процедура проводится для всех n элементарных отрезков. Величина 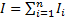принимается в качестве искомого значения интеграла. Условия (17) и соответствующий выбор величин обеспечивают выполнение условия