Выбор шага интегрирования по теоретическим оценкам погрешностей

Пусть требуется вычислить интеграл с точностью e. Тогда, используя формулу для R, выбирают шаг так, чтобы

| R | < e/2.

Учитывается также число знаков после запятой, чтобы погрешность округления не превышала e/2.

Пример. С помощью формулы Симпсона вычислить

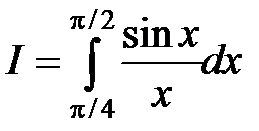
точностью e = 10^–3.

Решение. Выберем шаг h.

; x Î [ a, b ], т.е. x Î [p/4, p/2];

Согласно соотношений (23), получим

< 0,5×10^–3.

Вычислим f ^IV (x)

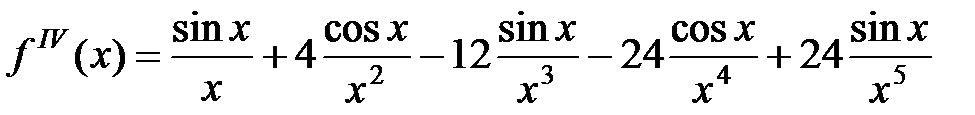
(24)

Оценим | f ^IV | на отрезке [p/4, p/2]. Воспользуемся величинами из (24)

И

Они положительные и убывают, следовательно, их максимальное значение в точке x = p/4. При этом

+ < 81.

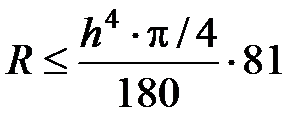
Таким образом, < 0,5×10^–3; h ⁴ < 14×10^–4; h £ 0,19.

С другой стороны для данного метода h выбирается с учетом того, чтобы [p/4, p/2] делился на четное число отрезков. Этим двум требованиям отвечает h =p/24 = 0,13 < 0,19, при котором

n = = 6.

Тогда, чтобы погрешность округления не превысила 0,5×10^–3 достаточно вычисления выполнить с 4 знаками после запятой.

Составим таблицу, с h = p/24 = 7° 30´ = 0,1309

i	xi0	xi	sin x	y0, y6	y2m	y2m–1
	45° 00´	0,7854	0,7071	0,9003
	52° 30´	0,9163	0,7934			0,8659
	60° 00´	1,0472	0,8660		0,8270
	67° 30´	1,1781	0,9239			0,7843
	75° 00´	1,3090	0,9659		0,7379
	82° 30´	1,4399	0,9914			0,6885
	90° 00´	1,5708	1,0000	0,6366
Сумма	1,5369	1,5649	2,3386

Для n = 6 по формуле Симпсона