Численное дифференцирование. Постановка задачи

Численное дифференцирование (ЧД) используют, когда нужно вычислить производные для функций, заданных таблично или когда непосредственное дифференцирование y = f (x) затруднительно.

Для нахождения в точке x области определения

функции нужно взять несколько близких к ней узлов x ₁, x ₂, …, x _n (n ³ m +1) (шаблон). Вычислить y _i= f (x _i) в узлах шаблона и построить интерполяционный многочлен Тогда

Интерполирование производится на равномерной сетке, и производные находятся в узлах x _i с соответствующей оценкой их погрешностей. При n = m +1 формулы ЧД не зависят от положения точки x внутри шаблона. Такие формулы называются простейшими формулами ЧД.

43.Аппроксимация производных посредством локальной интерполяции:

В случае табличного задания функции производная:

Полагая (1)

Соотношение (1) – аппроксимация производной с помощью отношения конечных разностей.

При заданных значениях таблицы { x_i, y_i }, i = и шаге расположения интерполяционных узлов h = const в зависимости от способа вычисления конечных разностей для i -го узла имеют место следующие алгоритмы вычисления (1). Пусть i = 1.

1. Формула левых разностей

(2)

2. Формула правых разностей

(3)

3. Формула центральных разностей

(4)

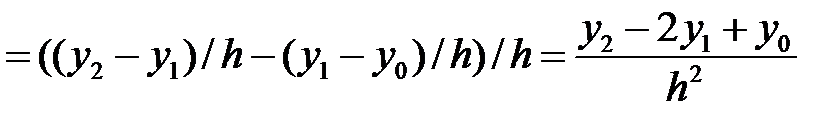Используя соотношения (2), (3), (4) последовательно можно получить выражения для вычисления производных высших порядков. К примеру, используя (3), получим:

(5)