Интерполяционные формулы для численного дифференцирования на основе многочлена Ньютона

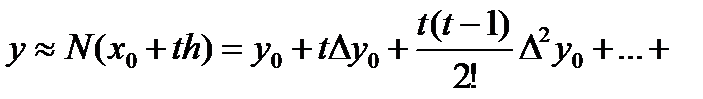Предположим, что функция f (x), заданная в виде таблицы с постоянным шагом h = x_i – x_{i– 1} (i = 1,2,…, n) может быть аппроксимирована интерполяционным многочленом Ньютона:

(9)

Дифференцируя (9) по переменной x как функцию сложную:

можно получить формулы для получения производных любого порядка:

(10)

Следует заметить, что точность ЧД для выбранного x будет существенно зависеть от значений функции во многих узлах, что не предусмотрено в соотношениях (2) – (4).

Замечание. В расчетной практике численного диффере-нцирования интерполяционные многочлены Ньютона, Гаусса, Стирлинга и Бесселя используются в несколько иной форме, так как формулы ЧД применяют для нахо-ждения производных в равностоящих узлах x_i = x₀ + ih (i = 0, ±1, ±2, …), то любую точку сетки можно принять за начальную и формулы ЧД записывают для точки x₀. А это равносильно подстановке в них t = (x – x₀)/ h = 0. Тогда дифференцирование многочленов приводит к следующим формулам.

По Ньютону:

(а)

(b)

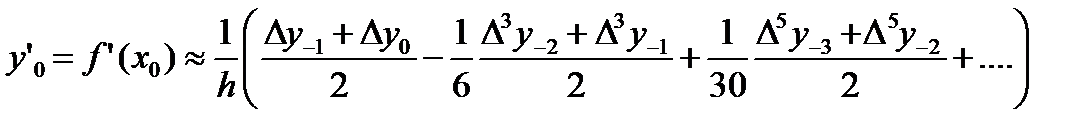Формулы (а) применяются для начальных строк таблиц, а (b) – для последних строк таблицы. Тогда по Стирлингу:

(c)

Формулы (с) – для дифференцирования в середине таблицы.