Интерполяционные формулы для численного дифференцирования на основе многочлена Лагранжа

Запишем интерполяционный многочлен Лагранжа L (x) и его остаточный член RL (x) для случая трех узлов интерполяции (n = 2), но с учетом, что x_i – x_i–1 = h = const (i = 1,2,..., n):

L (x) = [(x – x ₁)(x – x ₂)y₀ – 2(x – x ₀)(x – x ₂)y₁ +(x – x ₀)(x – x ₁)y₂];

R_L (x) = (x – x 0)(x – x ₁)(x – x ₂).

Найдем их производные:

L' (x) = [(2 x – x ₁ – x ₂)y₀ – 2(2 x – x ₀ – x ₂)y₁ +(2 x – x ₀ – x ₁)y₂];

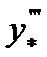R' _L(x) = [(x – x ₁)(x – x ₂) + (x – x ₀)(x – x ₂) + (x – x ₀)(x – x ₁)].

Здесь значение производной в некоторой внутренней точке x _* Î [ x ₀, x _n].

Запишем выражение для производной y' ₀ при х = x ₀:

y' ₀ = L' (x ₀) + R' _L(x ₀) = [(2 x ₀– x ₁– x ₂)y₀ – 2(2 x ₀– x ₀– x ₂)y₁ + (2 x ₀ – x ₀ – x ₁)y₂] + [(x ₀ – x ₁)(x ₀ – x ₂) + (x ₀ – x ₀)(x ₀

– x ₂) + (x ₀ – x ₀)(x ₀ – x ₁)] = (– 3y₀ + 4 y ₁ – y ₂) +

Аналогично можно получить значения y' ₁, y' ₂ при х = x ₁, х = x ₂.

Итак, для случая трех узлов (n = 2) рабочие формулы имеют следующий вид:

(11)

В справочных пособиях приведены формулы Лагранжа для n = 3, 4, …. Так для случая четырех узлов (n = 3):

(12)

Анализируя (11) и (12) можно утверждать, что, используя значения функции в (n +1) узлах, получают аппроксимацию n -го порядка точности для производной. Эти формулы можно использовать не только для узлов x ₀, x ₁, x ₂, …, но и для любых узлов x = x _i, x _i+1, x _i+2, … с соответствующей заменой индексов в (11) и (12). С помощью многочлена Лагранжа получены аппроксимации и для старших производных.

Таким образом, при n = 3:

Аналогичные формулы можно получить и для случая произвольной сетки расположения узлов. Однако в этом случае имеют место неизбежные громоздкие выражения для расчетов производных.

При возникшей необходимости таких расчетов целесообразнее применять искусственный прием, так называемый метод неопределенных коэффициентов.