Квадратурные формулы Гаусса-Кристофеля

Для класса функций высокой степени гладкости (f (x) Î C_k [ a, b ], k >2) имеет место явление насыщения численного метода.

Для них разработаны квадратурные формулы такого же типа, что и раньше но посредством их структурного реформирования путем подбора в них (2 n +1) параметров: n узлов x_i, n коэффициентов q_i и самого числа n.

математический аппарат подбора параметров: (Полиномы Лежандра построенные на [–1, 1])

(33)

рабочая квадратурная формула Гаусса (33) является точной (R = 0) для всех полиномов степени N = 2 n – 1.

Для практических целей искомые коэффициенты q_i и абсциссы x _i для произвольных n табулированы для формулы (33).

n	x i	qi
...	-x1= x4 = 0,861136312 -x2= x3 = 0,339981044	q 1 = q 4 = 0,347854845 q 2 = q 3 = 0,652145155
	-x1= x5 = 0,906179846 -x2= x4 = 0,538469310 x3 = 0	q 1 = q 5 = 0,236926885 q 2 = q 4 = 0,478628670 q 3 = 0,568888889
...

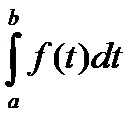
При вычислении интеграла следует сделать

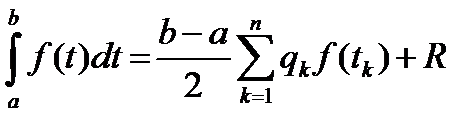замену переменной интегрирования:

t = x (b – a)/2 + (a + b)/2. Тогда (34)

где t_k = x_k (b – a)/2 + (b + a)/2, x_k – узлы формулы (33) на отрезке [–1;1] и q_k – соответствующие им коэффициенты, взятые из таблицы.