Замечания

1. Разные способы построения многочленов Лагранжа и Ньютона дают тождественные рабочие формулы при заданной таблице f (x). Это следует из единственности интерполяционного многочлена заданной степени на упорядоченной системе узлов.

2. Повышение точности интерполирования предположительно

проводить за счет увеличения числа узлов n и соответственно степени полинома P_n (x). Однако при таком подходе увеличивается погрешность из-за роста | f ^{( n )}(x) | и, кроме того, увеличивается вычислительная погрешность.

Эти соображения приводят к другому способу приближения функций с помощью сплайнов (будет рассмотрено дальше).

3. Повышение точности интерполирования осуществляется и посредством специального расположения узлов интерполяции на рассматриваемом отрезке [ a, b ] области определения функции f (x). Известно, что если сконцентрировать узлы x_i вблизи одного конца отрезка [ a, b ], то погрешность R_n (x) при длине отрезка l = b – a > 1 будет велика в точках x_i близких к другому концу. Поэтому всегда возникает задача о наиболее рациональном выборе x_i (при заданном числе узлов n).

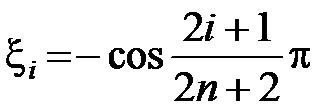
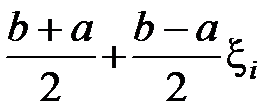Эта задача была решена Чебышевым, т.е. оптимальный выбор узлов нужно производить по формуле: x_i =

, где (i = 0,1,2,..., n) – есть нули полинома Чебышева T_{n +1}(x).

Ланграндж!

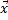, – одномерные массивы

известных значений x и f (x);

n – размер массивов,;

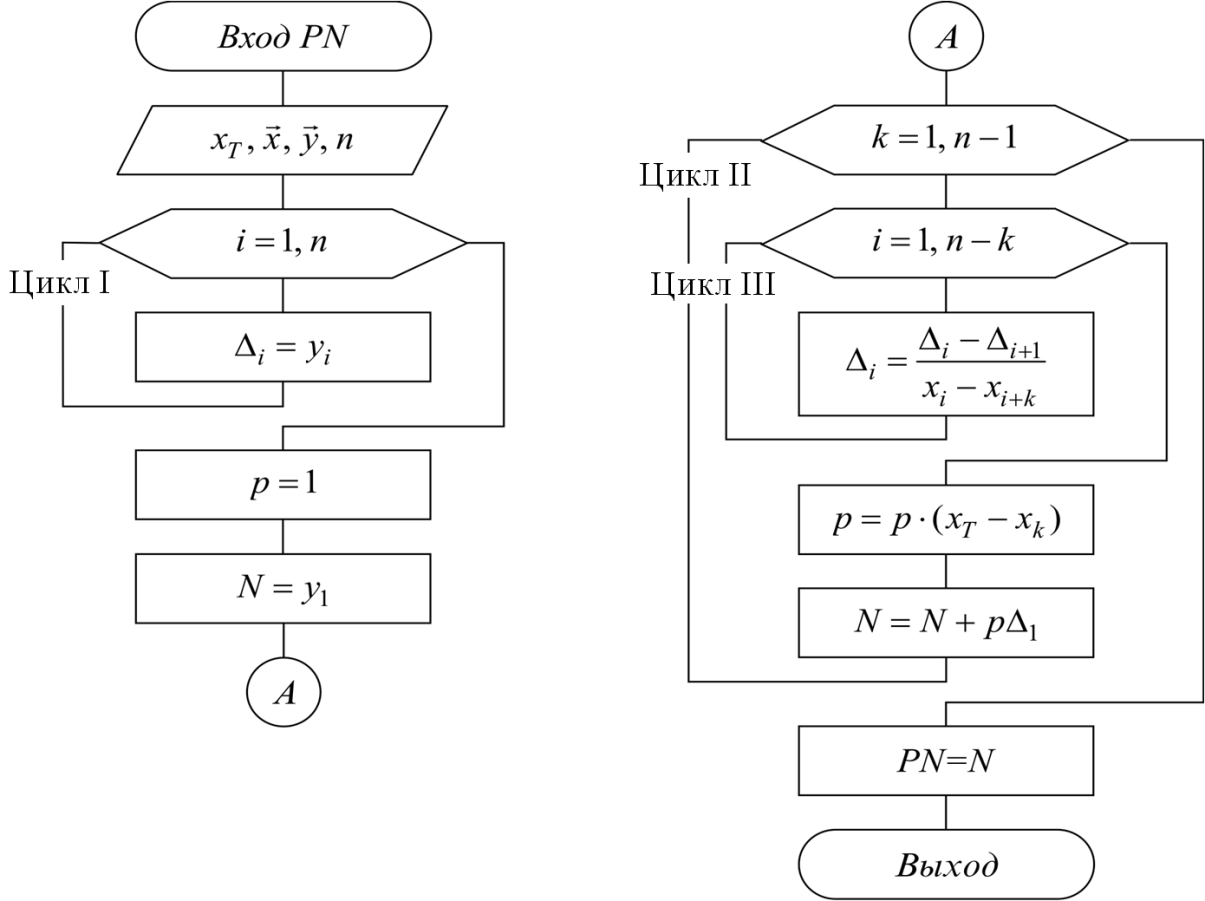
представлен на рис. 5.1.

В схеме введены следующие обозначения:

p – значение накапливаемой суммы,

результат которой равен L (x_Т);

e – значение очередного члена произведения;

Результатом функции PL является значение p

.

Ньютон

31.Сплайны:

Пусть интервал [ a, b ] разбит узлами x_i, как и выше, на n отрезков, 0 £ i £ n Сплайном S_n (x) называется функция, определенная на [ a, b ], принадлежащая C^k [ a, b ] и такая, что на каждом отрезке [ x_i, x_{i +1}], 0 £ i £ n –1 – это полином n -й степени.

В частности, это могут быть, построенные специальным образом, многочлены 3-й степени (кубический сплайн), которые являются математической моделью гибкого тонкого стержня, закреплен-ного в двух точках на концах с заданными углами наклона a и b.

В данной физической модели стержень принимает форму, минимизирующую его потенциальную энергию. Пусть форма стержня определяется какой-то функцией y = S (x). Из курса сопротивления материалов известно, что уравнение свободного равновесия имеет вид S ^(IV)(x) = 0. А этому состоянию соответствует многочлен третьей степени между двумя соседними узлами интерполяции. Его выбирают в виде

S (x) = a_i + b_i (x – x_{i –1}) + c_i (x – x_{i –1})² + d_i (x – x_{i –1})³; x_{i –1} £ х £ x_i. (31)

Стоит проблема нахождения a_i, b_i, c_i, d_i. Для определения их на всех n элементарных участках интервала [ a, b ] необходимо составить 4 n уравнений. Часть этих уравнений в составе 2 n получают из условия прохождения S (x) через заданные точки, т.е.

S (x_{i –1}) = y_{i –1}; S (x_i) = y_i .

Эти условия можно записать, используя (31) в виде:

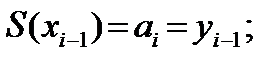
(32)

(33)

Уравнения в количестве (2 n –2) получают из условия непрерывности первых и вторых производных в узлах интерполяции. Условие гладкости.

Вычислим производные многочлена (31)

S ' (x) = b_i + 2 c_i (x – x_{i –1}) + 3 d_i (x – x_{i –1})²,

S " (x) = 2 c_i + 6 d_i (x – x_{i –1}); при x_{i –1} £ х £ x_i. (34)

Приравнивая в каждом внутреннем узле x = x_i значения этих производных, вычисленных на концах рассматриваемого отрезка, получают (2 n –2) уравнений

b_{i +1} = b_i + 2 h_ic_i + 3 h d_i; i =1,2,…, n –1; (35)

c_{i +1} = c_i + 3 h_id_i; i =1,2,…, n –1. (36)

Оставшиеся 2 уравнения получают из естественного предположения условия о нулевой кривизне этой функции на концах отрезка.

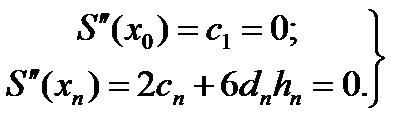(37)

Система, составленная из (32) – (37), решается одним из методов решения СЛАУ.

Для упрощения машинных расчетов эта система уравнений приводится к более удобному виду посредством следующего алгоритма.

1. Из условия (32) можно сразу найти a_i.

2. Из (36) – (37) находят:

(38)

3. После подстановки (38) и (32) в (33) находят

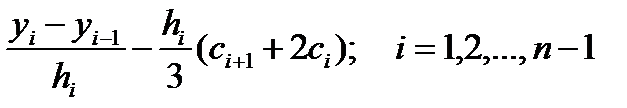коэффициенты b_i:

b_i =;

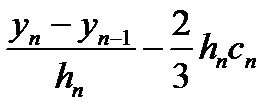
b_n =. (39)

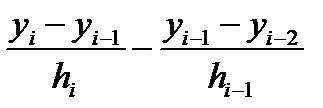4. Учитывая (38) и (39) из уравнения (35) исключаются d_i и b_i, тогда исходная система приводится к трехдиагональной матрице, содержащей только коэффициенты c_i. Получаем систему

h_{i –1} c_{i –1} + 2(h_{i –1} + h_i) c_i + h_ic_{i +1} = 3(), i =2,3,…, n. (40)

При этом c ₁ = 0, c_{n +1} = 0. Система (40) может быть решена методом прогонки. Зная c_i по (38) и (39), определяют b_i и d_i. Тогда кубический многочлен определяется для всех интервалов.

32.Метод наименьших квадратов:

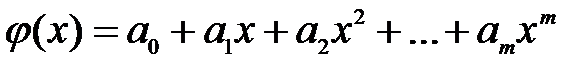В данном случае речь идет о среднеквадратичном приближении аппроксимируемой функции посредством многочлена:

(45)

’

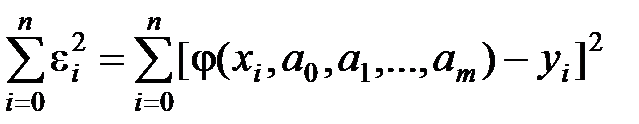при этом m £ n; случай m = n соответствует интерполяции. На практике, как правило, m = 1,2,3. Мерой отклонения j(x) от f (x) на множестве точек (x_i, y_i), (i =0,1,…, n), в данном случаи является соотношение по невязке

S =. (46)

Параметры ā, как независимые переменные, находятся из условия минимума функции S = S (a ₀, a ₁,…, a_{n –1}).

(47)

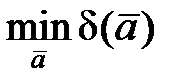
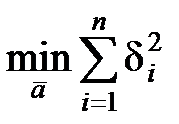
Система уравнений (47) трактуется следующим образом

= =.

Из системы (47) определяются параметры a ₀, a ₁, …, a_m. В этом и состоит метод наименьших квадратов (МНК).

33.Подбор эмпирических формул для интерполяций:

В случае невозможности обеспечения чистоты эксперимента, при получении табличных значений функции, нужно иметь в виду ошибки этих данных. Интерполирование усугубляет эти ошибки. В этом случае для аппроксимации прибегают к построению эмпирических формул, как моделей приближенных функциональных зависимостей. График эмпирических зависимостей не проходит через точки { x_i, y_i }. В результате экспериментальные данные как бы сглаживаются посредством подбора эмпирических формул.

Построение эмпирических формул состоит из 2-х этапов:

1) построение их общего вида;

2) определение наилучших значений содержащихся в них параметров.

1. Общий вид определяется из физических соображений. Если характер зависимостей неизвестен, то формулы выбираются

произвольно, сообразуясь с их простотой. Сначала они выбираются из геометрических соображений среди простейших функций.

2. Если эмпирические формулы подобраны, то они представляются в общем виде:

y = j(x, a₀, a₁,..., a_m); (41)

j – известная функция; a_i – неизвестные коэффициенты, которые и подбираются для лучшего приближения.

Тогда отклонение (невязка) определяется:

e _i = j(x_i, a ₀, a ₁,..., a_m) – y_i; i =. (42)

Задача нахождения a_i сводится к минимизации e _i. Существует несколько способов: метод выбранных точек, метод средних, метод наименьших квадратов.

34.Постановка задач для решения нелинейных уравнений:

Одной из важных практических задач при исследовании различных свойств математической модели в виде функциональной зависимости y = f (x) является нахождение значений x, при которых эта функция обращается в ноль, т.е. решение уравнения f (x) = 0. (1)

Как правило, точное решение его можно получить только в исключительных случаях, так как оно в большинстве случаев носит нелинейный характер. Нелинейные уравнения делятся на два класса:

1) алгебраические, содержащие только алгебраические выражения;

2) трансцендентные, содержащие и другие функции (тригонометрические, показательные, логарифмические и др.).

Методы решения нелинейных уравнений делятся на прямые и итерационные методы.

Прямые методы позволяют записать корни в виде некоторых конечных соотношений (формул) для простых тригонометрических, логарифмических, показательных и простейших алгебраических уравнений.

Однако подавляющее число практически значимых уравнений могут быть решено только итерационными методами, т.е. методами последовательных приближений (численными методами).

Решение уравнений (1) при этом осуществляется в два этапа:

1) определение местоположения, характера интересующего нас корня и выбор его начального значения;

2) вычисление корня с заданной точностью e, посредством выбранного какого-либо вычислительного алгоритма.

На первом этапе вначале определяют, какие корни требуется найти, например, только действительные или только положительные или наименьший корень и т.д. Затем находят отрезки из области определения функции y = f (x), взятой из (1), содержащие по одному корню.

Имеются различные подходы к решению данной задачи для обоих видов нелинейных уравнений.

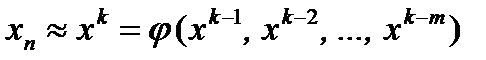На втором этапе используются итерационные методы, позволяющие с помощью некоторого рекуррентного соотношения

(6)

при выбранном начальном приближении к x ^* построить последовательность (x_n).

Как правило, всегда стоит задача обеспечения сходимости последовательности (2) к истинному значению корня x ^*. Сходимость достигается посредством выбора различными способами функций j в (2), которая зависит от f (x) и в общем случае от номера последовательности решений (n). При этом если при нахождении значения x_n» x^k » x ^*, используется одно предыдущее значение m =1, то такой метод называется одношаговым. Если используется m предыдущих значений, то метод называется m -шаговым и, как правило, с увеличением m вычислительные алгоритмы усложняются.

Расчет по рекуррентной последовательности продолжается до тех пор, пока | x_n – x_{n –1}| < e. Тогда последнее x_n выбирается в качестве приближенного значения корня (x ^* » x_n).

На практике имеется большой выбор законов j, что обеспечивает многообразие численных итерационных методов решения нелинейных уравнений.

35.Метод простой итерации для решения нелинейных уравнений:

Метод простой итерации применяется к решению уравнения (1), разрешенному относительно x:

x = j(x). (5)

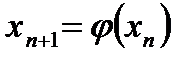Переход от записи (1) к эквивалентной записи (5) можно сделать многими способами.

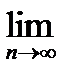Метод состоит в построении последовательности (2) в виде:, n = 0,1,2,….

Если j(x_n) – непрерывная функция, а x_n – сходящаяся последовательность, то искомое значение x * = x_n и будет решением (5), а, следовательно, и (1).

Например, получим (5) из (1) следующим образом: умножим (1) на подобранную специальным образом функцию y(x) ¹ 0 (в частности можно взять y(x) = const) и сложим с тождеством x = x, тогда (5) будет иметь вид, эквивалентный виду (3): (6)

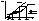Подбирая y(x) добиваются сходимости решения (6). Она может быть монотонной (если j'(x) > 0), или колеблющейся (если j'(x) < 0).

Метод, очевидно, является одношаговым (m =1)

и для начала вычислений нужно знать одно начальное

приближение x ₀ = a, или x ₀ = b, или x ₀ = (a+b)/2.

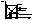
В методе простой итерации сходимость гарантированна не всегда, например, если j(x) имеет такой характер:

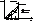
Такая ситуация может быть устранена подбором y(x) в (6).

Что касается выбора y(x), то можно взять, например, y(x) = Const = 1/ k. В этом случае необходимо, чтобы | k | > max| f ¢(x)| / 2. При этом знак k должен совпадать со знаком f ¢(x).

Доказано, что в общем случае расходимость (несходимость) исключается, если подбирается соотношение

При этом скорость сходимости увеличивается при уменьшении величины q.

Максимальный интервал (a, b) при выполнении условия (7) называется областью сходимости. Для данной оценки (7) берется любое x Î (a,b); x* Î(a,b).

Итерационный процесс уточнения корня заканчивается, когда {| x_n – x_{n –1}| или | f (x_n) – f (x_{n –1})|} < e.

36.Метод деления отрезка пополам для нелинейных уравнений:

Все вышеизложенные методы могут работать, если функция f (x) из (1) является непрерывной и дифференцируемой вблизи искомого корня, в противном случае решение не гарантируется. Данный метод может быть использован даже для разрывных функций.

Его алгоритм реализовывается согласно следующей рекуррентной последовательности: для x ^*Î [a,b]; x ₀ = a; x ₁ = b, находится x ₂ = (a+b)/2.

Очередная точка x ₃ выбирается как середина того из смежных с x ₂ интервалов [ x ₀, x ₂] или [ x ₂, x ₁], на котором находится корень. В результате получается следующий алгоритм метода деления отрезка пополам:

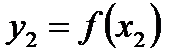
1) вычисляем y ₀ = f (x ₀);

2) вычисляем;

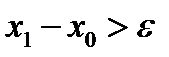3) если, тогда x ₀ = x ₂, иначе x ₁ = x ₂; (13)

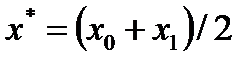4) если, тогда повторять с п. 1;

5) вычисляем.

За одно вычисление функции погрешность уменьшается вдвое, т.е. скорость сходимости невелика, однако метод устойчив к ошибкам округления и всегда сходится.

Немного подкорректировав алгоритм (13), его более наглядно можно представить в виде блок-схемы:

37.Метод хорд для нелинейных уравнений:

Пусть корень С уравнения f (x)=0 отделен на [ a, b ]. Функция f (x) непрерывна на отрезке и на его концах имеет разные знаки. Точки А и В имеют координаты соответственно (a, f (a)) и (b, f (b)).

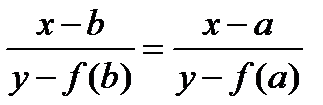Искомым корнем С будет пресечение f (x) с осью ОХ. В начале итераций вместо С ищется приближение x ₁, как результат пересечения ОХ с хордой АВ.

Уравнение прямой АВ запишем в виде.

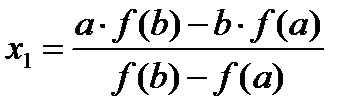
Полагая у = 0, находим. Это можно записать в виде:

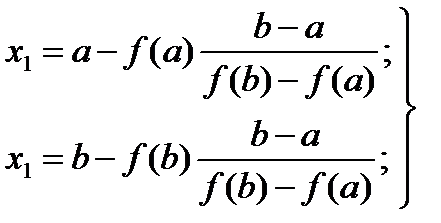
Или (14)

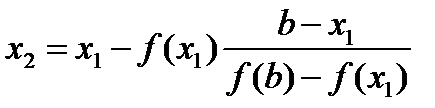Если x ₁ оказывается недостаточно точным, находят второе приближение:

(15)

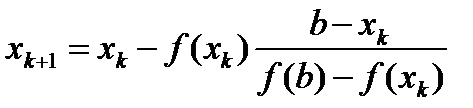На основании (14) и (15) можно записать рекуррентную последовательность:

, (16)

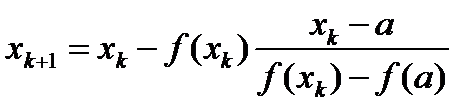
если, и (17) если.

Заметим, что на выделенном интервале [ a, b ] имеют место четыре типа расположения кривой f (x).

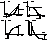
Для I-го f ' (x) > 0, f " (x) > 0;

для II-го f ' (x) < 0, f " (x) < 0;

для III-го f ' (x) > 0, f " (x) < 0;

для IV-го f ' (x) < 0, f " (x) > 0.

Тогда для I-го и для II-го используется (16), т.е. х ₀ = а. Для III-го и IV-го используется (17), т.е. х ₀ = b.

В заключение заметим, что во всех методах для определения функции f (x) и ее производных целесообразно использовать схему Горнера.

38.Метод касательных и его интерпретации:

Данный метод является модификацией метода простой итерации. Если функция f (x) непрерывна и дифференцируема, то выбрав в (6) получим эквивалентное уравнение в виде

x = x – f (x)/ f '(x) = j(x), f '(x) ¹ 0.

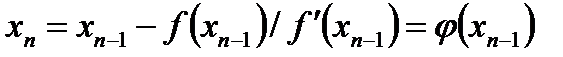Подбором y(x) добиваются, чтобы в (7) q = j'(x^*) º 0, что обеспечивает большую скорость сходимости в рекуррентном соотношении метода в близи искомого корня

, n = 1,2,… (8)

Это также одношаговый метод. Геометрическая интерпретация метода представлена на рисунке.

Проблематичным является выбор x ₀ в виду узости области сходимости вычисления производной. Часто при неудачном выборе x ₀ нет монотонного убывания последовательности | f (x_n)|, поэтому рекомендуется вычисления проверить по модифицированной схеме

n = 0,1,2,…

Здесь сомножители a _n Î [0,1] выбирают так, чтобы выполнялось неравенство | f (x_{n +1})| < | f (x_n)|.

При выборе начального приближения х ₀ предпочтительней использовать заведомо сходящийся метод, например, метод деления отрезка пополам.

39.Отделение корней для нелинейных уравнений графическим и аналитическим методом:

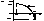Отделить корень х ^* уравнения f (x) = 0 – значит указать окрестность точки x ^*, не содержащую других корней этого уравнения.

Рис. 3.1

Как известно из анализа, если непрерывная функция f (x) на концах отрезка [ a, b ] принимает значения разных знаков, т.е. если f (a)× f (b) < 0, то внутри этого отрезка существует, по крайней мере, один корень уравнения f (x) = 0 (рис 3.1). При этом корень x * будет единственным, если f ' (x) сохраняет знак внутри интервала (а, b) (рис. 3.1 а).

На практике отделение корней уравнения f (x) = 0 на от-резке [ а, b ] и начинается с проверки условия f (a)× f (b) < 0. Если это условие выполнено, то, следовательно, на (a, b) имеется корень и дальнейшая задача состоит в выяснении его единственности или не единственности.

Для отделения корней практически достаточно провести процесс половинного деления, в соответствии с которым отрезок [ a, b ] делится на 2,4,8,… равных частей и последовательно определяются знаки функции в точках деления. При этом если в точках деления х_i, х_{i +1} выполнено условие f (х_i)× f (х_{i +1}) < 0, то на интервале (х_i, х_{i +1}) имеется корень уравнения f (x) = 0. При определении корней всегда стараются найти интервал (х_i, х_{i +1}) как можно меньшей длины.

Согласно вышеизложенному, получается следующий алгоритм определения корней уравнения f (x) = 0:

1) находим участки возрастания и убывания функции f (x) (с помощью производной f ¢(x), если она существует);

2) составляем таблицу знаков функции f (x) в стационарных точках (или ближайших к ним), а так же в граничных точках области определения f (x);

3) определяем интервалы по правилу x_i = a + (i – 1)×(b – a)/ m – 1; i = 1, 2, …, m, на которых f (x) имеет противоположные знаки. Внутри таких интервалов содержится только по одному корню. На рисунке 3.1 б интервалы монотонности функции (a, c), (c, d), (d, b), на концах которых функция имеет противоположные знаки.

Корнями уравнения f (x) = 0 на отрезке [ a, b ] в данном случае являются точки x ₁, x ₂ и x ₃.