Для системы равноотстоящих узлов

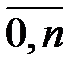В случае равностоящих узлов имеется много различных формул, построение которых зависит от расположения точки интерполирования х_Т по отношению к узлам интерполирования.

Пусть функция f(x) задана таблицей значений f_k = f(x_k) = y_k в узлах x_k=x₀+kh (k = ), h = x_k+1 – x_k = const.

На основании условий (3) и аппарата конечных разностей для определения коэффициентов для искомого многочлена (17) получена формула , k = ; при условии, что D⁰ = 1; 0! = 1. (22)

Подставляя (22) в (17) получим формулу Ньютона для интерполирования в начале таблицы

(23)

При этом конечные разности определяются или по схеме (табл.1) или по формуле для произвольного узла (19).

Для практического удобства формула (23) часто записывают в другом виде. Вводится новая переменная t = (x – x₀)/h. Тогда имеем: x = x₀ + kh;

’ …’

и (23) примет вид

N(x₀ + th) = y₀ + t . (24)

Выражение (24) может аппроксимировать y = f(x) на всем отрезке [x₀, x_n]. Однако, с точки зрения повышения точности расчетов, и уменьшения числа членов в (24), рекомендуется ограничиться случаем t < 1, т.е. использовать формулу (24) для интервала x₀ £ x £ x₁. Для других значений аргумента, например, для x₁ £ x £ x₂, вместо x₀ лучше взять значение x₁. Тогда (24) можно записать в виде

N(x_i+th) = y_i+ ; i = 0,1,…

(25)

Выражение (25) называется первым интерполяционным многочленом Ньютона для интерполирования вперед. Он используется для вычисления значений функций в точках левой половины рассматриваемого отрезка.

Это объясняется тем, что разности D^ky_i вычисляются через значение функции y_i, y_i+1, ..., y_i+k, причем i + k £ n. Поэтому при больших значениях i нельзя вычислить значения разностей высших порядков (k £ n – i). Например, при i = n – 3 в (25) можно учесть только Dy, D²y, D³y.

Для правой половины отрезка разности рекомендуется вычислять справа налево. В этом случае t = (x – x_n) / h, т.е. t < 0 и (25) можно получить в виде

N(x_n + th) = y_n +

(26)

Полученная формула называется вторым интерполяционным многочленом Ньютона для интерполирования назад. Для интерполирования в средине отрезка можно использовать интерпретации многочлена Ньютона – это многочлены Стирлинга, Гаусса, Бесселя. Погрешность метода Ньютона:

при t = , x – принадлежит отрезку.