Полином Лагранжа на системе равноотстоящих

интерполяционных узлов

Величина h = x_{i +1} – x_i = const. Тогда произвольный узел x_i = x ₀+ i × h,. Введем переменную t = (x – x ₀)/ h. Тогда x – x_i = x ₀ + th – x ₀ – ih = (t – i) h. (15)

Подставив разности (15) в равенство (11) получим:

Далее, так как

x_j – x_i = (x ₀ + jh) – (x ₀ + ih) = (j – i) h,

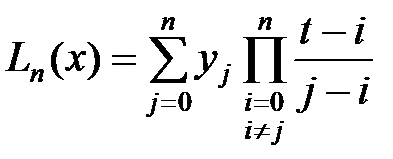то с учетом (15) формула Лагранжа примет вид:

(16)

где t = (x – x ₀)/ h.

Его погрешность

30.Интерполяционный многочлен Ньютона:

27.Понятия конечных разностей для задач аппроксимации:

28.Понятия разделенных разностей для задач аппроксимации:

Как и в предыдущем случае строится многочлен (2) с соблюдением условий (3) специфического вида. Интерполяционный многочлен Ньютона ищется в следующем виде:

N (x)= a ₀+ a ₁(x – x ₀)+ a ₂(x – x ₀)(x – x ₁)+…+ a_n (x – x ₀)(x – x ₁)…(x – x_{n –1}). (17)

Как и в случае (8) для получения рабочей формулы Ньютона необходимо определить значения коэффициентов a_i. В отличие от технологии расчета (9) для построения интерполяционного многочлена Ньютона вводится рабочий аппарат в виде, так называемых, конечных разностей для системы равноотстоящих интерполяционных узлов и в виде разностных отношений (разделенные разности) для произвольной системы узлов.

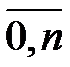Пусть заданны равноотстоящие узлы x_k = x ₀ + kh, h = x_{i +1} – x_i = const > 0. Значения f (x) в них обозначим f (x_k) = f_k = y_k, k =.

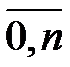Конечными разностями первого порядка принято называть величины D f (x_i) = D f_i = f_{i +1} – f_i; i =.

Конечные разности второго порядка определяются равенствами

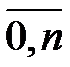i =.

Конечные разности (k +1)-го порядка определяются через разности k -го порядка

i =; k =. (18)

Конечные разности, как правило, вычисляются по следующей схеме:

Таблица 1

i	fi	Dfi	D2fi	D3fi	…
	f0
		Df0
	f1		D2f0
		Df1		D3f0
	f2		D2f1
		Df2		D3f1
	f3		D2f2
		Df3
	f4
…	…

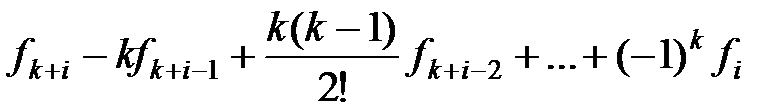Каждая последующая конечная разность получается путем вычитания в предыдущей колонке верхней строки из нижней строки. Последняя колонка D ^kf_i будет равна нулю. Заметим, что конечные разности можно выразить непосредственно через значения функций. Так для i -го узла рабочая формула имеет вид:

D ^kf_i = (19)

i =; k = 1,2,...

Разностными отношениями (разделенными разностями) первого порядка называются величины

f (x ₀, x ₁)= f (x ₁, x ₂)=;...

Здесь x_i – произвольные узлы с соблюдением приоритетности по величине.

По этим соотношениям составляются разностные отношения второго порядка:

f (x ₀, x ₁, x ₂) =; f (x ₁, x ₂, x ₃) =;…

Разделенные разности порядка (k +1), k = 1,2,... определяются при помощи разделенных разностей предыдущего порядка k по формуле:

f (x ₀, x ₁, …, x_{k +1}) =. (20)

Разностные отношения вычисляются по следующей схеме:

Таблица 2

i	xi	fi	f(xi,xi+1)	f(xi,xi+1,xi+2)	…
	x0	f0
			f(x0,x1)
	x1	f1		f(x0,x1,x2)
			f(x1,x2)
	x2	f2		f(x1,x2,x3)
			f(x2,x3)
	x3	f3		f(x2,x3,x4)
…	…	…	…	…	…

Для равноотстоящих узлов x_k = x ₀ + kh (k =) имеет место соотношение между разделенными разностями и конечными разностями

f (x ₀, x ₁, …, x_k) = k = 0,1,2, … (21)

Конечная разность и разделенная разность порядка n от многочлена степени (n) равны постоянной величине, и, следовательно, они для более высокого порядка равны нулю.