 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уточнение корней
|
|
Полученные методом Гаусса приближенные значения корней можно уточнить.
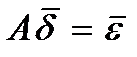
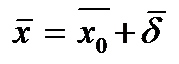
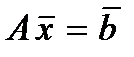Пусть для системы найдено приближенное решение, не удовлетворяющее по «невязке». Положим тогда Для получения поправки d = (d1, d2,..., dn)Т корня следует рассмотреть новую систему
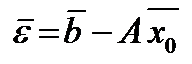
или
где – невязка для исходной системы.
Таким образом, решая линейную систему с прежней матрицей А и новым свободным членом = (e1, e2,..., e n)Т, получим поправки (d1, d2,..., d n).
15.Метод прогонки:
Данный метод также является модификацией метода Гаусса для частного случая разреженных систем – систем с матрицей трехдиагонального типа (краевая задача ДУ).
Каноническая форма их записи
aixi –1 + bixi + cixi +1 = di; i =; a 1 = cn = 0, (9)
или в развернутом виде
b 1 x 1 + c 1 x 2 = d 1;
a 2 x 1 + b 2 x 2 + c 2 x 3 = d 2; (10)
a 3 x 2 + b 3 x 3 + c 3 x 4 = d 3;
...
an –1 xn –2 + bn –1 xn –1 + cn –1 xn = dn –1;
anxn –1 + bnxn = dn.
При этом, как правило, все коэффициенты bi ¹ 0.
Метод реализуется в два этапа – прямой и обратный ходы.
Прямой ход
Каждое неизвестное xi выражается через xi +1
xi = Ai × xi +1+ Bi для i = 1,2,..., n –1, (11)
посредством прогоночных коэффициентов Ai и Bi. Определим алгоритм их вычисления.
Из первого уравнения системы (10) находим x 1
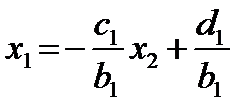
Из уравнения (11) при i =1: x 1= A 1× x 2+ B 1. Следовательно
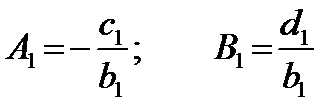
(12)
Из второго уравнения системы (10) определяем x 2 через x 3, подставляя найденное значение x 1
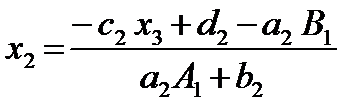а 2(A 1 x 2+ B 1) + b 2 x 2 + c 2 x 3 = d 2,
откуда (12*)
и согласно (11) при i = 2: x 2= A 2× x 3+ B 2, следовательно
где е 2= а 2× А 1+ b 2.
Ориентируясь на соотношения индексов при коэффициентах (12) и (12*) можно получить эти соотношения для общего случая
где еi = аi × Аi –1+ bi (i =2,3,..., n –1) (13)
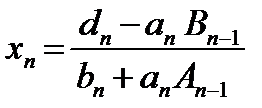Обратный ход. Из последнего уравнения системы (10) с использованием (11) при i = n –1
(14)
Далее посредством (11) и прогоночных коэффициентов (12), (13) последовательно вычисляем xn –1, xn –2,..., x 1.
При реализации метода прогонки нужно учитывать, что при условии
| bi | ³ | ai | + | ci | (15)
или хотя бы для одного bi имеет место строгое неравенство (15), деление на «0» исключается и система имеет единственное решение.
Заметим, что условие (15) является достаточным, но не необходимым. В ряде случаев для хорошо обусловленных систем (10) метод прогонки может быть устойчивым и при несоблюдении условия (15).
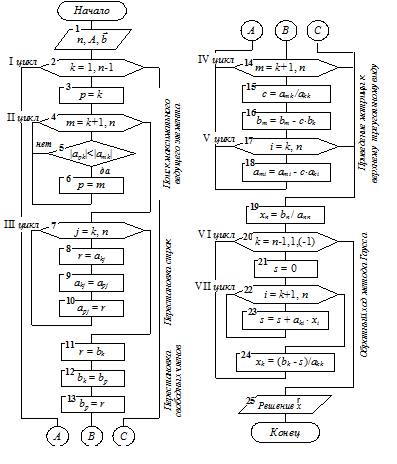
Схема алгоритма метода прогонки может иметь вид, представленный на рис. 2.2.
16.Метод квадратного корня:
Данный метод используется для решения линейной системы (16)
у которой матрица А симметрическая, т.е. АТ = А,
aij = aji (i = j =1,..., n).
Решение системы (16) осуществляется в два этапа.
Прямой ход.
Преобразование матрицы А и представление ее в виде произведения двух взаимно транспонированных треугольных матриц: А = S Т × S (17)
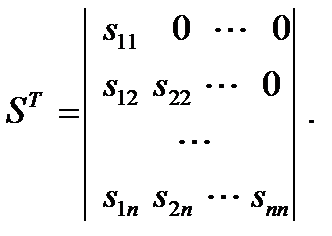
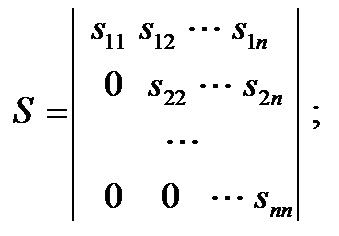где
Перемножая SТ и S, и приравнивая матрице А, получим следующие формулы для определения sij:
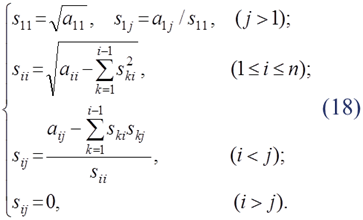
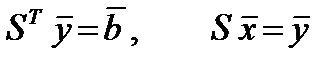После нахождения матрицы S систему (16) заменяем двумя ей эквивалентными системами с треугольными матрицами (17)
(19)
Обратный ход.
Записываем системы (19) в развернутом виде:
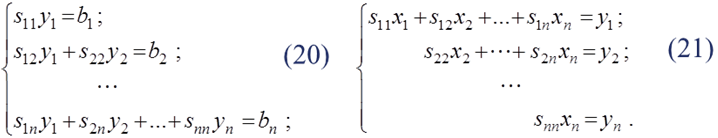
Используя (20) и (21) последовательно находим
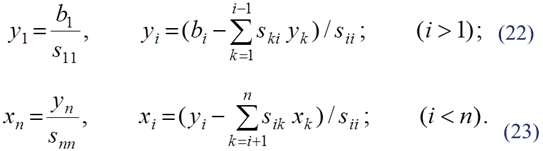
Метод квадратных корней дает большой выигрыш во времени по сравнению с рассмотренными ранее прямыми методами, так как, во-первых, существенно уменьшает число умножений и делений (почти в два раза), во-вторых, позволяет накапливать сумму произведений без записи промежуточных результатов.
Машинная реализация метода предусматривает его следующую трактовку. Исходная матрица А системы (16) представляется в виде произведения трех матриц
A = S Т × D × S,
где D – диагональная матрица с элементами dii = ±1; S – верхняя треугольная (sik = 0, если i > k, причем sii > 0); ST – транспонированная нижняя треугольная.
Требование выполнения условия sii > 0 необходимо для полной определенности разложения. Это и определяет необходимость введения диагональной матрицы D.
Блок-схема метода квадратного корня:
17.Метод простой итерации решения СЛАУ:
//*Напомним, что достоинством итерационных методов является их применимость к плохо обусловленным системам и системам высоких порядков, их самоисправляемость и простота реализации на ЭВМ. Итерационные методы для начала вычисления требуют задания какого-либо начального приближения к искомому решению.
Следует заметить, что условия и скорость сходимости итерационного процесса существенно зависят от свойств матрицы А системы и от выбора начальных приближений.
Для применения метода итераций исходную систему (1) или (2) необходимо привести к виду
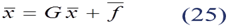
и затем итерационный процесс выполняется по рекуррентным формулам
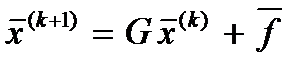, k = 0, 1, 2,.... (25*)
Матрица G и вектор получены в результате преобразования системы (1).
Для сходимости (25*) необходимо и достаточно, чтобы |l i (G)| < 1, где l i (G) – все собственные значения матрицы G. Сходимость будет также и в случае, если || G || < 1, ибо |l i (G)| < " || G || (" – любой).
Символ ||... || означает норму матрицы.*//
Технология итерационного решения вида (25*) названа методом простой итерации.
Оценка абсолютной погрешности для метода простой итерации
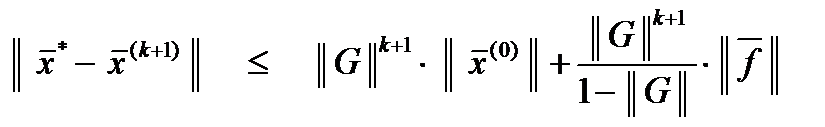
напомним, символ ||... || означает норму.
Пример 1. Методом простой итерации с точностью e=0,001 решить систему линейных уравнений
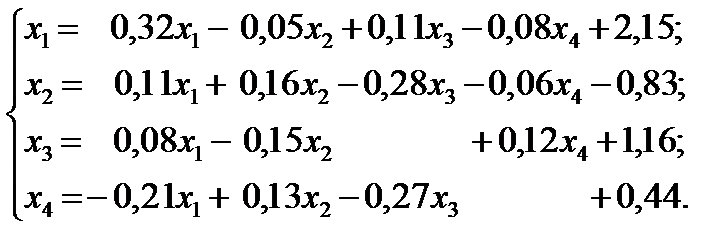
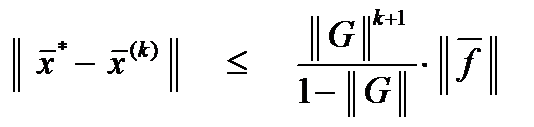Число шагов, дающих ответ с точностью до e = 0,001, можно определить из соотношения
£ 0,001
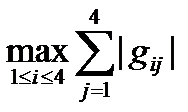
Оценим сходимость по формуле (26). Здесь || G || = =
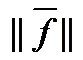= max{0,56; 0,61; 0,35; 0,61} = 0,61 < 1;
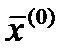= 2,15. Значит, сходимость обеспечена.
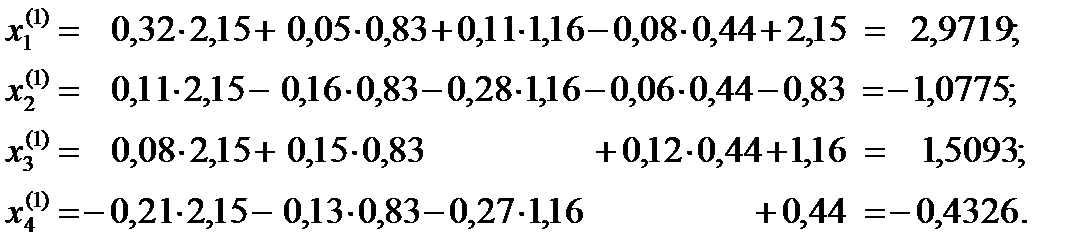
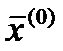В качестве начального приближения возьмем вектор свободных членов, т.е. = (2,15; –0,83; 1,16; 0,44)Т. Подставим значения вектора в формулы (25*):
Продолжая вычисления, результаты занесем в таблицу:
| k | х 1 | х 2 | х 3 | х 4 |
| 2,15 | –0,83 | 1,16 | 0,44 | |
| 2,9719 | –1,0775 | 1,5093 | –0,4326 | |
| 3,3555 | –1,0721 | 1,5075 | –0,7317 | |
| 3,5017 | –1,0106 | 1,5015 | –0,8111 | |
| 3,5511 | –0,9277 | 1,4944 | –0,8321 | |
| 3,5637 | –0,9563 | 1,4834 | –0,8298 | |
| 3,5678 | –0,9566 | 1,4890 | –0,8332 | |
| 3,5760 | –0,9575 | 1,4889 | –0,8356 | |
| 3,5709 | –0,9573 | 1,4890 | –0,8362 | |
| 3,5712 | –0,9571 | 1,4889 | –0,8364 | |
| 3,5713 | –0,9570 | 1,4890 | –0,8364 |
Сходимость в тысячных долях имеет место уже на 10-м шаге.
Ответ: х 1» 3,571; х 2» –0,957; х 3» 1,489; х 4» –0,836.
Это решение может быть получено и с помощью формул (27*).
18. Метод Зейделя-Гаусса:
Данный метод является модификацией метода простой итерации и для системы (25) имеет следующую технологию (32):
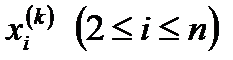Суть его состоит в том, что при вычислении
очередного приближения
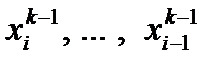в системе (32) и в формуле (27*),
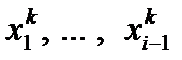если имеет место соотношение (27), вместо
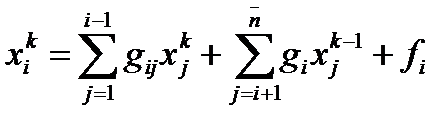используются уже вычисленные ранее, т.е. (27*)
преобразуется к виду, i = 1, …, n. (33)
Это позволяет ускорить сходимость итераций почти в два раза. Оценка точности аналогична методу простой итерации. Схема алгоритма аналогична схеме метода простой итерации, если x 0 j заменить на xj и убрать строки x 0 i = 1, x 0 i = xi.
Замечание. Если для одной и той же системы методы простой итерации и Зейделя сходятся, то метод Зейделя предпочтительнее. Однако на практике имеет место ситуация, когда области сходимости этих методов могут быть различными, т.е. метод простой итерации сходится, а метод Зейделя расходится и наоборот. Для обоих методов, если близка к единице, скорость сходимости очень малая.
Для ускорения сходимости тогда используется искусственный прием – так называемый метод релаксации. Суть его заключается в том, что полученное по методу итерации очередное значение пересчитывается по формуле:
w – как правило, принято изменять в пределах 0 < w £ 2 с каким-то шагом (можно h = 0,1 или 0,2). Параметр w подбирают так, чтобы сходимость метода достигалась за минимальное число итераций.
Релаксация – (физ.тех.) постепенное ослабление какого-либо состояния тела после прекращения действия факторов вызвавших это состояние.
19.Вычисление определителей:
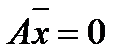В отличие от технологии вычисления определителей в методе Крамера, для матриц общего вида, являющихся элементом СЛАУ, для решения этой задачи успешно может использоваться метод Гаусса. Прямой ход метода для системы позволяет вычислить
так как последовательное исключение элементов величину определителя не изменяет. Здесь аkk – элементы преобразованной матрицы А (прямой ход Гаусса).
Знак зависит от четности или нечетности перестановок строк исходной матрицы при приведении ее к треугольному виду во избежание делении на «0» или необходимости поиска «max» ведущего элемента в текущем столбце на каждом этапе исключение неизвестных.
Для симметричных матриц:
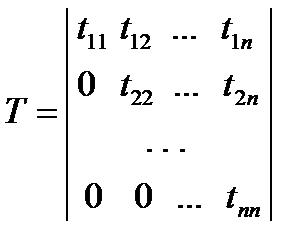
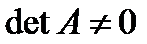20.Вычисление обратных матриц:
1. По методу Гаусса. Всякая неособенная матрица, для которой, имеет обратную матрицу. Очевидно, что А * А –1 = Е. запишем это равенство в виде системы n уравнений с n неизвестными
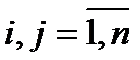
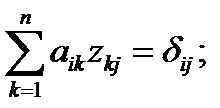
(37)
Где аik – элементы матрицы А;
zkj – элементы обр. матрицы (А –1);
dij – элементы единичной матрицы.
При этом dij =
Для нахождения элементов одного столбца обратной матрицы необходимо решить соответствующую линейную систему (37) с матрицей А. Так для получения j -го столбца для А –1 (z 1 j, z 2 j,… znj) решается система:
(38)
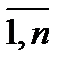
Следовательно для обращения матрицы А нужно n раз решить систему (38) при j =. Поскольку матрица А системы не меняется, то исключение неизвестных осуществляется только один раз, а (n –1) раз при решении (38) делается только обратный ход с соответствующим изменением правой ее части.
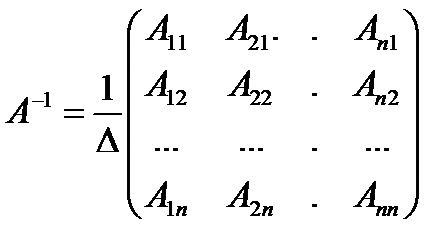2. Другой подход к определению обратной матрицы А–1
где D – определитель матрицы, Аij – алгебраические дополнения соответствующих элементов матрицы А.
3. Обращение матрицы А посредством треугольных матриц
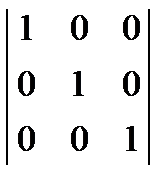Известно, что всякая обратная матрица, если она существует, то по структуре будет такая же, как и исходная, т.к. А –1× А = А × А –1 = Е = (39)
21.Метод итераций для уточнения элементов обратных матриц:
Точность получения элементов обратной матрицы естественно оценивается соотношением
А –1× А = А 0 = Е.
Однако в общем случае элементы обратной матрицы получаются с некоторой погрешностью, которая появляется в результате округлений в процессе вычисления и большого числа арифметических операций. Для уменьшения погрешностей используется итерационная схема уточнения элементов обратной матрицы.
Пусть для неособенной матрицы А получено приближенное значение элементов матрицы А –1. Обозначим ее через D 0» A –1. Тогда для уточнения элементов обратной матрицы строится следующий итерационный процесс:
Fk –1 = E – ADk –1, k =1,2,3…; (*)
Dk = Dk –1(E + Fk –1); k = 1,2,3… (**)
Доказано, что итерации сходятся, если начальная матрица D 0 достаточно близка к искомой А –1.
В данной итерационной схеме матрица F на каждом шаге как бы оценивает близость матрицы D к А –1.
Схема работает следующим образом.
Сначала по (*) при k = 1 находится F 0 = E – AD 0, затем находится произведение D 0 F 0.
По итерации (**) при k = 1 находится D 1= D 0 + D 0 F 0.
Чтобы проверить, достигнута ли желаемая точность, вычисляется AD 1, а по (*) при k = 2, вычисляется F 1 = E – AD 1 и, если наибольший элемент матрицы F 1 < e, итерации прекращаются и A–1» D 1.
22.Постановка задачи для аппроксимации функциональной зависимости:
При решении многих практических задач часто приходится вычислять значения каких-то функциональных зависимостей y = f (x).
При этом, как правило, имеют преобладающее место две ситуации.
1. Явная зависимость между х и y на [ a, b ] отсутствует, а имеется только таблица экспериментальных данных { xi, yi }, i= 
и возникает необходимость определения y = f (x) на интервале [ xi, xi /2] Î [ a, b ]. К этой задаче относится также уточнение таблиц экспериментальных данных.
2. Зависимость y = f (x) известна и непрерывна, но настолько сложна, что не пригодна для практических расчетов. Стоит задача упрощения вычисления значений y = f (x) и ее характеристик (f’(x), max f(x),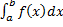 
и т.д.). Поэтому, с точки зрения экономии времени и материальных ресурсов, приходят к необходимости построения какой-то другой функциональной зависимости y = F (x), которая была бы близка к f (x) по основным ее параметрам, но более проста и удобна в реализации при последующих расчетах, т.е. ставится задача о приближении (аппроксимации) в области определения y = f (x). Функцию y = F (x) называют аппроксимирующей.
23.Виды аппроксимирующих функций:
Основной подход к решению данной задачи заключается в том, что y = F (x) выбирается зависящей от каких-то свободных параметров эксперимента, т.е. y = F (x) = j(x, c 1, c 2, …, cn) = j(x,). Значения вектора выбираются из каких-то условий близости для f (x) и F (x).
B зависимости от способа подбора вектора, получают различные виды аппроксимации. Если приближение строится на каком-то дискретном множестве { xi }, то аппроксимация называется точечной. К ней относится интерполирование, среднеквадратичное приближение (МНК). Если множество { xi } непрерывно, например, в виде отрезка [ a, b ], аппроксимация называется непрерывной или интегральной (полиномы Чебышева).
В настоящее время на практике хорошо изучена и широко применяется линейная аппроксимация, при которой j(x,) выбирается линейно-зависящий от параметров в виде так называемого обобщенного многочлена:
F (x) = j(x,) = c 1j1(x) + c 2j2(x) + … + cn j n (x) =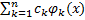 
; (1)
здесь j k (x) – какая-то выбранная линейно-независимая система базисных функций. В качестве их могут быть, например,
– алгебраическая: 1, x, x 2,..., xn,...;
– тригонометрическая: 1, sin(x), cos(x),… sin(nx), cos(nx),…;
– экспоненциальная: e a0 x, e a1 x, …, e a nx, …;
где {a i } – некоторая числовая последовательность попарно различных действительных чисел.
Важным является, чтобы эта система была полной, т.е. обеспечивающей аппроксимацию посредством (1) c заданной точностью на всех интервалах [ а, b ] определения y = f (x).
24.Интерполирование функций:
Интерполирование по определению предполагает нахождение промежуточных значений величины заданной таблицей или графиком по некоторым ее значениям. Относительно функциональных зависимостей она является одним из основных видов точечной аппроксимации. Суть интерполирования в данном случае заключается в следующем:
Пусть функция f (х) определена на отрезке [ а, b ], на котором должна быть обеспечена близость f (х) и j(х). На данном отрезке выбирается система точек, называемых узлами, по правилу:
a £ x 0 < x 1 < x 2 < … < xn £ b.
Их число равно количеству параметров с в (1).
Известны значения функции f (х) в этих узлах, т.е.
yi = f (xi),
Задача интерполирования сводится к подбору многочлена согласно (1) вида:
(2)
с действительными коэффициентами сk, найденными по правилу:
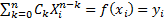, i= 
(3)
Такой многочлен называют интерполяционным многочленом.
Процедуру (2) с использованием условий (3) называют глобальной интерполяцией. Если же многочлен (2) строится только для отдельных участков отрезка [ а, b ] (области определения f (х)), т.е. для m интерполяционных узлов, где m < n, то интерполяцию называют локальной.
Матрица системы (3) и ее определитель имеют следующий вид:
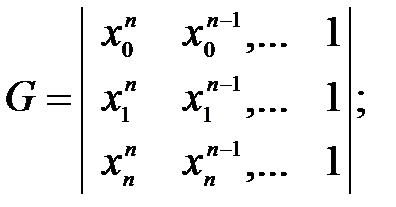
|G|≠0; (4)
так как узлы выбранной системы точек различны. Следовательно, система (3) имеет единственное решение, т.е. коэффициенты многочлена (2) находятся однозначно.
Заметим, что условие (3) обеспечивает близость f (х) и F (х), по любой технологии ее получения, т.е. в узлах интерполяции f (х) и F (х) совпадают по их значениям.
Если (2) и (3) используются для вычисления значений функции для случая x < x 0 и x > xn такое приближение называется экстраполяцией.
25.Линейная и квадратичная интерполяция:
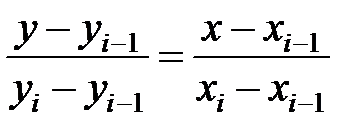Линейная интерполяция состоит в том, что заданные точки таблицы (xi, yi), i= соединяются прямыми линиями и исходная функция f (х) приближается на интервале [ а, b ] к ломаной с вершинами в узлах интерполяции. В общем случае частичные интервалы [ xi– 1, xi ] Î [ a, b ] различны. Для каждого отрезка ломаной можно написать уравнение прямой, проходящей через точки (xi –1, yi –1) и (xi, yi). В частности, для i -го интервала в виде:
Тогда рабочую формулу можно записать:
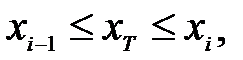
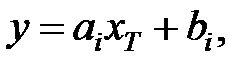(5)
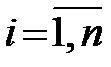
где
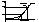
Из графической иллюстрации видно, что для
реализации (5) сначала нужно определить интервал,
в который попадает значение xT,
а затем воспользоваться его границами.
Теоретическая погрешность R (x) = f (x) – F (x) ¹ 0
в точках, отличных от узлов.
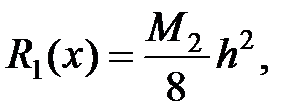
где М 2=max, х Î [ xi– 1, xi ].
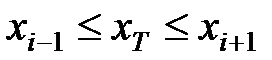
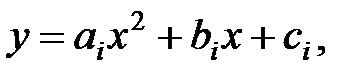В данном случае в качестве интерполяционного многочлена используется квадратный трехчлен на отрезке [ xi– 1, xi+ 1] Î [ а, b ] в виде:
(6)
Для определения коэффициентов ai, bi, ci составляется система из трех уравнений согласно условиям (3), а именно:
(7)
Алгоритм вычисления аналогичен предыдущему, только вместо соотношений (5) используется соотношение (6) с учетом решения (7). Очевидно, что для xT Î [ x 0, xn ] используются три ближайшие точки.
Графическая иллюстрация метода
Теоретическая погрешность вне узлов интерполяции
R (x) = (x – x 0) × (x – x 1) × (x – x 2) 
26.Виды глобальной интерполяции:
Дата публикования: 2014-10-20; Прочитано: 3610 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
