Коефіцієнти Лагранжа. Оцінка похибки інтерполяції

Вираз 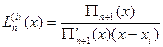(1) називається коефіцієнтами Лагранжа. Тоді многочлен Лагранжа набере вигляду: 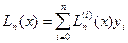(2). Зауважимо, що форма коефіцієнтів Лагранжа інваріантна відносно лінійної підстановки: 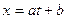. Це означає, що якщо 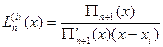, то отримаємо: .

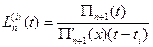У випадку рівновіддалених вузлів інтерполяції вираз для коефіцієнтів Лагранжа спрощується.

Нехай 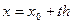, , 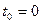,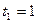…, , 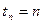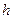- деякий крок.

,

,

.

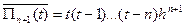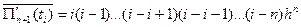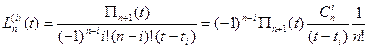Тоді 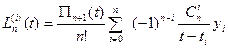.(3)

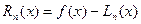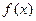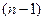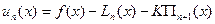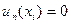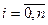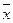
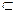
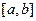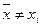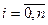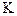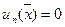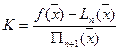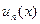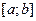Оцінимо похибку . Нехай існують похідні функції до порядку включно, розглянемо функцію: . Очевидно, що для всіх . Візьмемо деяку точку : , . Підберемо так, щоб , тобто .(4) Тоді функція на має 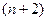корені і на кінцях відрізків 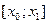, ,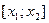…, , 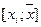,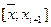…, 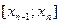приймає однакові нульові значення. За теоремою Рімана 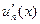має принаймні 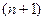нуль або більше, 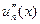має 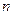нулів,..., 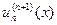має хоча б один нуль.

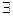
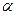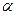
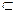
Нехай : 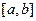і 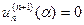. Оскільки 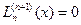, , 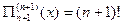тому 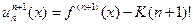. Підставимо точку 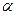: 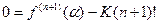,(5)

,

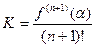
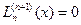з (4) і (5) слідує:

.

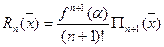Внаслідок довільності вибору точки 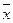і позначивши 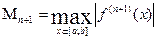, отримаємо 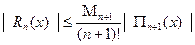(6)

Де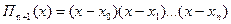

Приклад:

З якою точністю можна обчислити 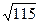за допомогою формули Лагранжа для функції 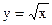, якщо за вузли вибрано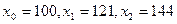

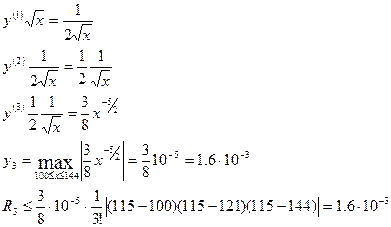
Скориставшись формулою Лагранжа для задачі, то похибка різниці на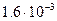

§4