Многочленами Ньютона

Нехай нескінченно-диференційовна на 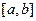функція 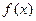задана своїми значеннями в точках , 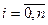. Замінимо цю функцію на 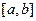першим інтерполяційним поліномом Ньютона:

Врахувавши, що похідна:

Зауваження: за 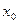слід вибирати вузол інтерполяції, який знаходиться найближче до точки 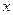, в якій шукаємо похідну.

Якщо потрібно знайти похідну в вузлі інтерполяції, тоді , .

§10

ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ ІНТЕРПОЛЬОВАНИХ МНОГОЧЛЕНАМИ ЛАГРАНЖА.

Залишимо в силі умови попереднього параграфа. Замінимо функцію 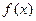інтерполяційним многочленом:

, поділимо кожну дужку на 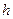і домножимо на .

тоді ,

,

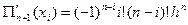підставимо .

Тоді . Похибка у випадку многочлена Лагранжа рівна: ,

.

У випадку, коли , тоді .

Зауваження: часто похибка, яка виникає при обчисленні похідних може набагато перевищувати похибку задання самої функції(навіть може зростати до ).

Наприклад: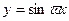

§11