Методи розв’язування нелінійних систем

Нехай задана система рівнянь:

(1)

1). МЕТОД НЬЮТОНА.

По методу Ньютона послідовність наближень будують за формулою:

(2)

- матриця обернена до матриці Якобі. Для системи двох рівнянь з двома невідомими формули (2) наберуть вигляд: , .

.

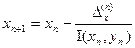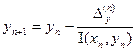За початкове наближення вибираємо точку, яка знаходиться якомога ближче до розв’язку.

2). МЕТОД ПРОСТОЇ ІТЕРАЦІЇ.

Нехай маємо систему:

(3)

або (), яка рівносиль системі (1).

Ітерації будуємо користуючись формулою: (4)

Щоб звести f(x)=0 до () потрібно, щоб .

Тоді .

У випадку функції двох змінних, отримаємо: ,

.

шукають з системи:

Зауваження: метод ітерації буде збіжним, якщо виконується умови:

або

.

Тоді оцінку похибки проводять за формулою: ,

де або .

Розділ 3

§1

Постановка задачі інтерполяції

Нехай на сегменті [a;b] задана система (n+1) точок: . Їх називають вузли інтерполяції. Задано також значення в цих точках деякої функції: , ,….., . Потрібно побудувати деяку функцію (інтерполяційну функцію), яка належить деякому класу функцій і таку, що: , ,….., .

Геометрично це означає: потрібно побудувати деяку криву певного типу, яка проходить через задану систему точок. Ці точки називаються вузлами інтерполяції.

Отриману інтерполяційну функцію використовуємо для знаходження значень функції 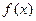в точках відмінних від вузлів інтерполяції. Така операція називається інтерполяція функцій.

Виділяють також поняття екстраполяції функції. Це той випадок, коли шукаємо значення функції 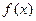в точці, яка не належить [a;b].

§2

ІНТЕРПОЛЯЦІЙНА ФОРМУЛА ЛАГРАНЖА.

На відрізку [a;b] задана система точок і задано значення функції 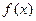в цих точках (, , ,….., ). (1)

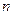Потрібно побудувати поліном степеня не вище , , такий що: 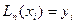, 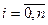.(2)

Спочатку побудуємо поліном , такий що (3). Оскільки на [a;b] згаданий поліном має 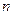нулів, тому цей поліном можна записати у вигляді: .

Підставивши , отримаємо:

. (4)

Знайденні підставимо в (3)

Тоді: . (5)

Будуємо многочлен (6)

або

.(7)

Очевидно, що степінь цього многочлена Лагранжа .

, .

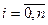Формулу (7) можна записати в компактному вигляді:

,

.

Підставивши , отримаємо:

.

Врахувавши останні позначення, отримаємо:

.

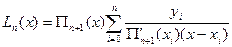При многочлен Лагранжа - пряма, яка проходить через точки ,

.

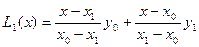Приклад: для функції побудувати многочлен Лагранжа, взявши вузли інтерполяції , , .

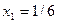§3