Ітераційний метод Зейделя

Даний метод це модифікований метод простої ітерації.

Нехай задана зведена лінійна система: (1). Виберемо деяке початкове наближення 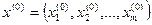вважаючи, що n – те наближення відоме, будемо шукати (n+1) наближення за таким принципом: .

Як правило метод Зейделя дає кращу збіжність, ніж метод простої ітерації. Бувають випадки коли метод Зейделя збіжний, а метод простої ітерації розбіжний і навпаки.

§10

ДОСТАТНІ УМОВИ ЗБІЖНОСТІ ІТЕРАЦІЙНИХ ПРОЦЕСІВ

Нехай маємо лінійну систему 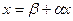.(1)

Означення: нормою матриці називається додатнє число, яке задовольняє наступні умови:

ü , ,

ü , ,

ü ,

ü .

Означення: норму матриці називають канонічною, якщо крім вище перерахованих умов виконуються умови:

ü ,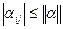

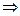
ü , де .

Найчастіше користуються наступними трьома нормами:

,

,

.

Теорема: процес ітерації для системи (1) збігається до єдиного розв’язку, якщо для деякої канонічної норми матриці виконується умова .