 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение краевой задачи для обыкновенного дифференциального уравнения методом конечных разностей
|
|
Задание: Используя метод конечных разностей, составить решение краевой задачи для обыкновенного дифференциального уравнения с точностью
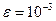 ; шаг
; шаг 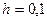 ;
;
Вариант №1
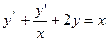 ;
;  ;
;
Вариант №2
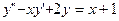 ;
; 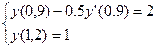 ;
;
Вариант №3
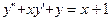 ;
; 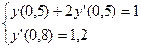 ;
;
Вариант №4
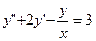 ;
;  ;
;
Образец выполнения задания:
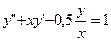 ;
; 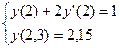 ;
;
Разбив отрезок 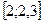 на части с шагом
на части с шагом 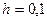 , получим четыре узловые точки с абсциссами:
, получим четыре узловые точки с абсциссами: 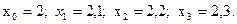 . Две точки являются конечными, а две другие внутренними. Данное уравнение во внутренних точках замени конечно-разностным уравнением:
. Две точки являются конечными, а две другие внутренними. Данное уравнение во внутренних точках замени конечно-разностным уравнением:
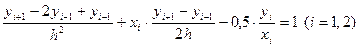 .
.
Из краевых условий составим конечно-разностные уравнения в конечных точках:
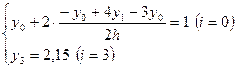
Данная задача сводится к решению системы уравнений:
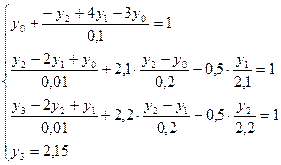
Выполнив преобразования, имеем:
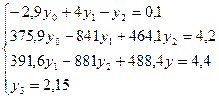
Поставив значение 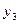 в третье уравнение, получим для определения остальных неизвестных систему:
в третье уравнение, получим для определения остальных неизвестных систему:


Для решения полученной системы воспользуемся, например, схемой «главных элементов».
| 
| 
| 
| Свободные члены | S |
| -0,00113507 -1 | -2,9 375,9 | -841 391,6 | -1 464,1 -881 | 0,1 4,2 -1045,66 | 0,2 3,2 -1535,06 |
| 0,00560179 -1 | -2,9 375,9 | 3,55551 -643,7098 | - - | 1,28690 -546,6411 | 1,94240 -805,4511 |
| -1 | -0,79429 | - | - | -1,77527 | -2,56957 |
| 2,2350 3,2351 | 2,1849 3,1849 | 2,1580 3,1580 |
Ответ:
| x | y | x | y |
| 2.0 2.1 | 2.235 2.185 | 2.2 2.3 | 2.185 2.150 |
Лабораторная работа 24
«Численные методы поиска минимума функции нескольких переменных»
1.Минимизировать функцию в Е^2 методом градиентного спуска с дроблением шага (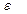 =0,05)
=0,05)
1)f(x,y)=2x+y+ 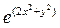
2) f(x,y)=1.5x+1.1y+ 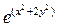
3) f(x,y)=0.5x+2y+ 
4) f(x,y)=1.8x+0.4y+ 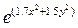
5) f(x,y)=3x+2y+ 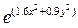
Пример: 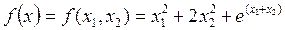
Следим, чтобы выполнялось условие монотонности 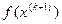 <
< 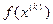
и вычисляем, пока не будет выполняться условие 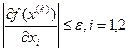
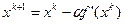
В качестве начального приближения 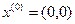 и
и 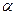 =1.
=1.
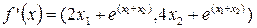
k=0; 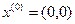 ;
; 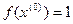 ;
; 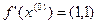 ;
; 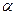 =1;
=1;
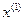 =
= 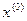 -
- 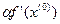 =(0, 0) – (1, 1) =(-1, -1)
=(0, 0) – (1, 1) =(-1, -1)
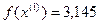 >
> 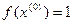 - условие монотонности нарушено
- условие монотонности нарушено
Уменьшаем 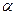 в 2 раза
в 2 раза 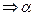 =0.5
=0.5
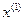 =
= 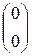 – 0,5
– 0,5 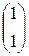 =
= 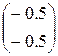
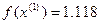 >
> 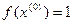 - условие монотонности нарушено
- условие монотонности нарушено
Уменьшаем 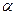 в 2 раза
в 2 раза 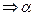 =0.25
=0.25
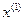 =(0, 0) –0.25 (1,1)=(-0,25,-0,25)
=(0, 0) –0.25 (1,1)=(-0,25,-0,25)
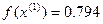 <
< 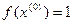 - условие монотонности выполняется
- условие монотонности выполняется
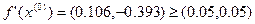
Условие останова не выполнено.
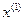 =(-0,25,-0,25),
=(-0,25,-0,25), 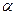 =0,25
=0,25
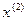 =(-0,25,-0,25)-0,25
=(-0,25,-0,25)-0,25 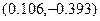 =(-0,277,-0,152)
=(-0,277,-0,152)
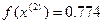 <
< 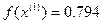 - условие монотонности выполняется
- условие монотонности выполняется
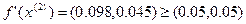
Условие останова не выполнено.
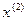 =(-0,277,-0,152)
=(-0,277,-0,152) 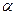 =0,25
=0,25
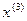 =(-0,277,-0,152)-0.25
=(-0,277,-0,152)-0.25 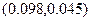 =(-0.301,-0.162)
=(-0.301,-0.162)
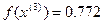 <
< 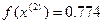 - условие монотонности выполняется
- условие монотонности выполняется

Условие останова выполнено.
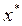 =(-0.301,-0.162),
=(-0.301,-0.162), 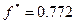
2.Минимизировать квадратичную функцию в Е^2 методом наискорейшего спуска(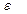 =0,01):
=0,01):
Квадратичная функция имеет вид: f(x)=1/2(Ax,x)-(b,x);
A-симметричная, положительно определенная матрица n*n, x 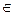 Е^2,b
Е^2,b 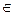 Е^2.
Е^2.
Ax= 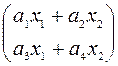 ; (Ax,x)=
; (Ax,x)= 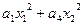 +
+  ;
;
(b,x)= 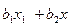
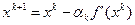
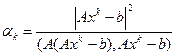
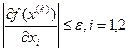
Для случая Е^2 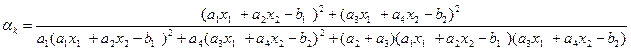
Пример:
В качестве начального приближения 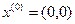
A= 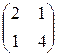 ; b=
; b= 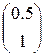 то
то 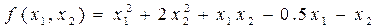
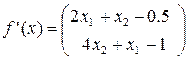
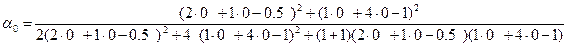 =0,227273
=0,227273
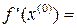
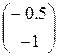
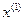 =
= 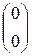 – 0,227273
– 0,227273 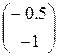 =
= 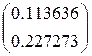
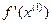 =
= 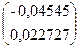

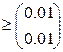
Условие останова не выполнено
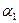 =0.625
=0.625
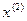 =
= 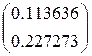 – 0.625
– 0.625 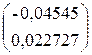 =
= 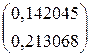
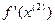 =
= 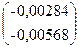

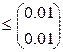
Условие останова выполнено.
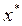 =
= 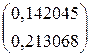 ,
, 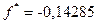
1) A= 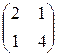 ; b=
; b= 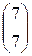
2)A=  ; b=
; b= 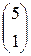
3)A= 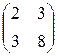 ; b=
; b= 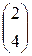
4)A= 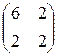 ; b=
; b= 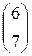
5) A= 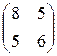 ; b=
; b= 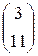
3. Минимизировать квадратичную функцию в Е^2 методом сопряжённых градиентов:
Примеры:
1. 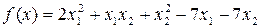
2. 
3. 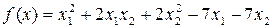
4. 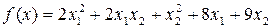
5. 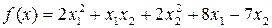
Квадратичная функция имеет вид: f(x)=1/2(Ax,x)-(b,x);
A-симметричная, положительно определенная матрица n*n, x 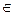 Е^2,b
Е^2,b 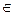 Е^2.
Е^2.
Ax= 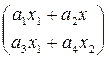 ; (Ax,x)=
; (Ax,x)= 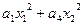 +
+  ;
;
(b,x)= 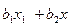
Пример:
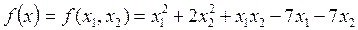
f(x) – квадратичная функция в E^2. Поэтому x* должна быть найдена после 2-х итераций метода сопряжённых градиентов.
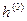
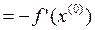 .
.
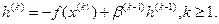
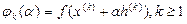 .
.
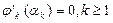 .
.
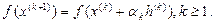
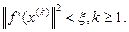
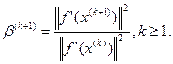
Пусть начальное приближение 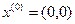 .
.
1-ая итерация: k=0
1. 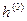
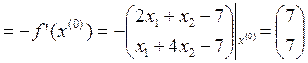
2. 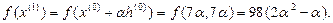
Решаем задачу минимизации 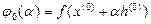 по α. Из условия минимума
по α. Из условия минимума 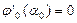 получим
получим  . Отсюда находим
. Отсюда находим
3. 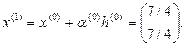
4. 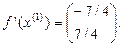
5. 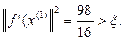
Условие остановки не выполнено.
2-ая итерация: k=1
6. 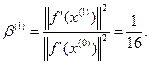
7. 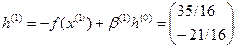
8. 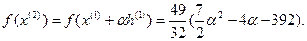
Решаем задачу минимизации 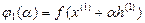 по α. Из условия минимума
по α. Из условия минимума  получим
получим 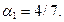
9. 
10. 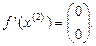
11. 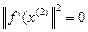 , тогда x*=
, тогда x*= 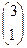 – решение задачи.
– решение задачи.
4. Минимизация функции F(x) методом барьерных функций:
Пример:
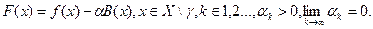
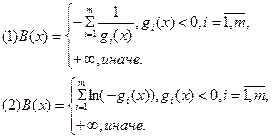
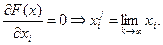
Пример:
1. 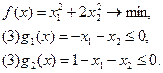
По (1):
Последовательность задач безусловной минимизации принимает вид:
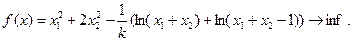
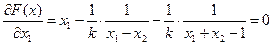
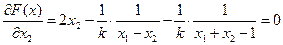
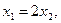
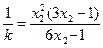
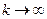
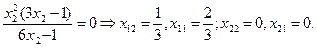
 принадлежит заданной области (3),а
принадлежит заданной области (3),а 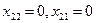 не принадлежит, тогда x*=(1/3,2/3) - решение.
не принадлежит, тогда x*=(1/3,2/3) - решение.
Дата публикования: 2014-11-18; Прочитано: 2139 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
