 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лабораторная работа18
|
|
Ортогональные многочлены Чебышева
Задание:
- На множестве точек
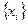 определить ортогональные многочлены Чебышева и вычислить их нормы.
определить ортогональные многочлены Чебышева и вычислить их нормы. - Требуется аппроксимировать функцию
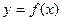 алгебраическими многочленами наилучшего среднеквадратического приближения
алгебраическими многочленами наилучшего среднеквадратического приближения 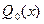 ,
, 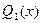 ,
, 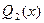 ,
, 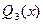 .
.
Вариант №1
1. 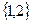
|
Вариант №2
1. 
|
Вариант №3
1. 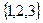
|
Вариант №4
1. 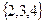
|
Вариант №5
1. 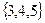
|
Вариант №6
1. 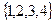
|
Образец выполнения задания:
1. 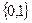
Многочленами Чебышева на множестве точек 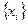 (
(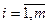 ) называются алгебраические многочлены, ортогональные на этом множестве, с нормой
) называются алгебраические многочлены, ортогональные на этом множестве, с нормой 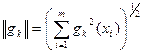 (
( ), отличной от нуля, и определяемые следующими рекуррентными формулами:
), отличной от нуля, и определяемые следующими рекуррентными формулами:
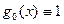
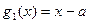
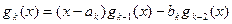 (
( )
)
 (
(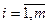 )
)
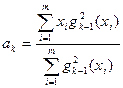

В данном примере 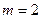 . Имеем
. Имеем
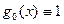 ;
; 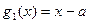 ;
; 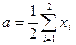
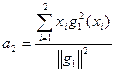 ;
; 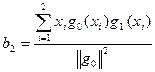
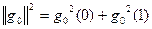
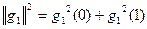
| i | xi | a | g0(xi) | g02(xi) | g1(xi) | g12(xi) | xig12(xi) | xig0(xi)g1(xi) | a2 | b2 |
| -0,5 | 0,25 | |||||||||
| 0,5 | 0,25 | 0,25 | 0,5 | |||||||
| Сумма | 0,5 | 0,25 | 0,5 | |||||||
| 0,5 | 0,5 | 0,25 |
Далее, используя рекуррентные соотношения, построим функцию
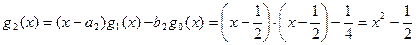 .
.
| i | xi | g2(xi) |
| -0,5 | ||
| 0,5 | ||
| Сумма |
Норма функции 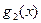 на множестве
на множестве 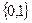 не равна нулю и, следовательно, эта функция является многочленом Чебышева.
не равна нулю и, следовательно, эта функция является многочленом Чебышева.
2.
| i | ||||
| xi | ||||
| yi |
Составим ортогональные многочлены Чебышева 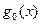 ,
, 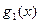 ,
, 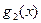 ,
,  на множестве точек
на множестве точек 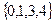 . Имеем
. Имеем
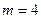
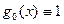 ;
; 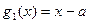 ;
; 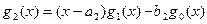 ;
; 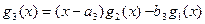
| i | xi | a | g02(xi) | g12(xi) | g22(xi) | g32(xi) | a2 | b2 | a3 | b3 |
| 2,25 | 1,44 | |||||||||
| 2,25 | 5,76 | |||||||||
| 2,25 | 5,76 | |||||||||
| 2,25 | 1,44 | |||||||||
| Сумма | 14,4 | |||||||||
| 2,5 | 0,9 |
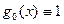 ;
; 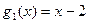 ;
; 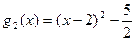 ;
; 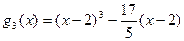
| i | xi | g0(xi) | g1(xi) | g2(xi) | g3(xi) |
| -2 | 1,5 | -1,2 | |||
| -1 | -1,5 | 2,4 | |||
| -1,5 | -2,4 | ||||
| 1,5 | 1,2 |
Многочлены наилучшего приближения имеют вид:
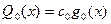 ,
, 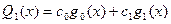 ,
, 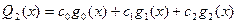 ,
, 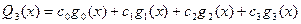 .
.
Здесь коэффициенты Фурье определены по формуле:
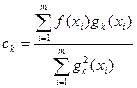 (
( )
)
| i | xi | g0(xi) | g1(xi) | g2(xi) | g3(xi) | xig0(xi) | xig1(xi) | xig2(xi) | xig3(xi) | c0 | c1 | c2 | c3 |
| -2 | 1,5 | -1,2 | -8 | -4,8 | |||||||||
| -1 | -1,5 | 2,4 | |||||||||||
| -1,5 | -2,4 | -1,5 | -2,4 | ||||||||||
| 1,5 | 1,2 | 2,4 | |||||||||||
| Сумма | -3 | 7,5 | -4,8 | ||||||||||
| 1,75 | -0,3 | 0,833 | -0,33 |
Квадрат наименьшего среднеквадратического отклонения:
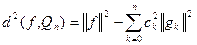
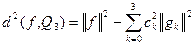
| i | yi | yi2 | c02 | c12 | c22 | c32 |
| Сумма | ||||||
| 3,063 | 0,09 | 0,69 | 0,111 |
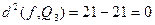
Тем самым найдены алгебраические многочлены наименьшего среднеквадратического приближения 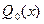 ,
, 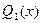 ,
, 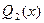 ,
, 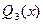 :
:
| i | xi | g0(xi) | g1(xi) | g2(xi) | g3(xi) | c0 | c1 | c2 | c3 | Q0 | Q1 | Q2 | Q3 |
| -2 | 1,5 | -1,2 | 1,75 | 2,35 | 3,6 | ||||||||
| -1 | -1,5 | 2,4 | 1,75 | 2,05 | 0,8 | ||||||||
| -1,5 | -2,4 | 1,75 | 1,45 | 0,2 | |||||||||
| 1,5 | 1,2 | 1,75 | 1,15 | 2,4 | |||||||||
| Сумма | |||||||||||||
| 1,75 | -0,3 | 0,833 | -0,33 |
Отметим, что 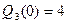 ,
, 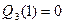 ,
, 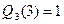 ,
, 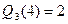 .
.
Дата публикования: 2014-11-18; Прочитано: 431 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
