 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритм нахождения собственных векторов линейного оператора
|
|
1. Найти собственные значения линейного оператора каксобственныезначения его матрицы 
2. Для каждого из найденных собственных значений l0 находимсобственные векторы, решая однороднуюсистему линейныхуравнений (*) с основной матрицей M (j) – λ0 E.
3. Множество 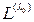 равно линейной оболочкефундаментального набора решений этой системы за исключением нулевого вектора.
равно линейной оболочкефундаментального набора решений этой системы за исключением нулевого вектора.
Пример 9.7. Найти собственныевекторылинейного оператора с матрицей M (j) = 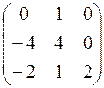 .
.
Решение. Находим собственные значения матрицы линейного оператора, для чего решаем уравнение | M (j) – λ E | = 0.
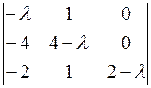 = (2–l)(–1)3 + 3
= (2–l)(–1)3 + 3 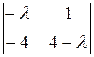 = (2 – l)((–l)(4 – l) – (–4)) =
= (2 – l)((–l)(4 – l) – (–4)) =
= (2 – l)(l2 – 4l + 4) = (2 – l)(l – 2)2 = (2 – l)3 = 0 Þ l1 = l2 = l3 = 2.
Итак, получили f (λ) = (2 – l)3 – характеристический многочлен матрицы M (j); (2 – l)3 = 0 – характеристическое уравнение матрицы M (j); l1 = l2 = l3 = 2 – собственные значения матрицы M (j), т. е. это собственные значения линейного оператора j.
Собственное значение у этого линейного оператора только одно, поэтому решаем только одну однороднуюсистему линейныхуравненийс матрицей 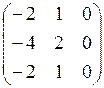 .
.
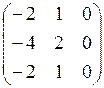 ~
~  ~
~ 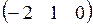 .
.
Выпишемобщее решение этой системы х 1 = 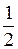 (х 2 + 0 х 3) и составим фундаментальный набор решений
(х 2 + 0 х 3) и составим фундаментальный набор решений
| х 1 | х 2 | х 3 | |
| с 1 | |||
| с 1 |
с 1= (1, 2, 0), с 2= (0, 0, 1).
Ответ. Множество собственных векторов с собственным значениемλ = 2 это множество L = L (с 1, с 2)\{ o } = { k 1 c 1 + k 2 c 2,  }.
}.
Дата публикования: 2014-11-18; Прочитано: 908 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
