 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Приведение матрицы к жордановой (нормальной) форме
|
|
Теорема 10.3. Жорданова нормальная форма определяется для матрицы однозначно с точностью до порядка расположения жордановых клеток на главной диагонали.
Приведем матрицу A (λ) = A – λ E к каноническому виду с помощью элементарных преобразований.
A – λ E = 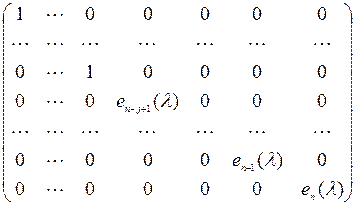 .
.
Отличные от единицы многочлены en – j +1(λ), …, en –1(λ), en (λ) называют инвариантными множителями матрицы A (λ). Среди них нет многочленов равных нулю, сумма степеней всех этих многочленов равна n, и все они раскладываются на линейные множители над множеством комплексных чисел. Пусть en – j +1(λ) раскладывается в произведение следующих множителей: 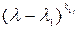 ,
, 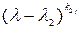 , …,
, …, 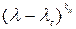 . Назовем эти множители элементарными делителями многочлена en – j +1(λ).
. Назовем эти множители элементарными делителями многочлена en – j +1(λ).
Определение 10.7. Элементарными делителями матрицы A (λ) называются элементарные делители всех многочленов en – j +1(λ), …, en –1(λ), en (λ).
Выпишем жорданову матрицу J порядка n, составленную из жордановых клеток определяемых следующим образом: каждому элементарному делителю  матрицы A (λ) ставим в соответствие жорданову клетку порядка kij, относящуюся к числу l i.
матрицы A (λ) ставим в соответствие жорданову клетку порядка kij, относящуюся к числу l i.
Пусть для некоторой матрицы порядка 9 характеристическая матрица A – λ E приведена к каноническому виду.
A – λ E = 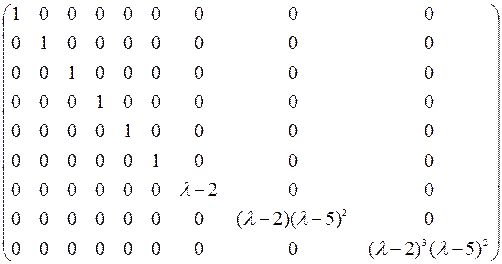 .
.
e 1 = e 2 = e 3 = e 4 = e 5 = e 6 = 1, e 7 = l – 2, e 8 = (l – 2)(l – 5)2, e 9 = (l – 2)3(l – 5)2 – инвариантные множители матрицы A – λ E, (l – 2), (l – 2), (l – 5)2,
(l – 2)3, (l – 5)2 – элементарные делители матрицы A – λ E.
Получаем: две клетки порядка 1, относящиеся к числу 2, две клетки порядка 2, относящиеся к числу 5, одну клетку порядка 3, относящуюся к числу 2, Выпишем жорданову форму матрицы A
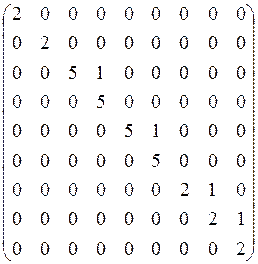
Алгоритм приведения матрицы A к жордановой форме
1. Составить характеристическую матрицу A – λ E.
2. Привести эту матрицу к канонической форме с помощью элементарных преобразований.
3. Разложить диагональные многочлены на линейные множители.
4. Найти элементарные делители и по ним выписать жорданову форму матрицы A.
Для того чтобы заданная матрица была подобна диагональной матрице, необходимо и достаточно, чтобы все элементарные делители ее характеристической матрицы были первой степени.
Пример 10.4. Привести к жордановой форме матрицу A = 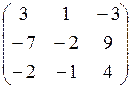 .
.
Решение. с помощью элементарных преобразований приводим матрицу A –λ E к следующему виду: A –λ E = 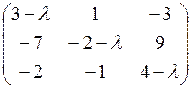 ~
~
~ … ~  . Инвариантные множители этой матрицы: e 1 = 1, e 2 = 1, e 3 = (l – 1)(l – 2)2; элементарные делители будут (l – 1),
. Инвариантные множители этой матрицы: e 1 = 1, e 2 = 1, e 3 = (l – 1)(l – 2)2; элементарные делители будут (l – 1),
(l – 2)2.
По найденным элементарным делителям выписываем жорданову форму исходной матрицы 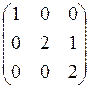 .
.
Дата публикования: 2014-11-18; Прочитано: 12685 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
