 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Обратимые линейные операторы
|
|
Определение 9.12. Линейныйоператор j называется обратимым, если существуетлинейныйоператорψтакойчто выполняетсяравенство j×ψ = ψ×j= e, где e – тождественный оператор.
Теорема 9.10. Если линейныйоператорj обратим,тооператорψопределяется единственным образом и называетсяобратнымдляоператора j.
В этом случае оператор, обратный для оператораj, обозначается j–1.
Теорема 9.11. Линейный операторj обратим тогда и только тогда, когда обратима его матрица M (j), при этом M (j–1) = (M (j))–1.
Из этой теоремы следует, что ранг обратимого линейного оператора равенразмерностипространства, а дефект равен нулю.
Пример 9.41) Определить, обратим ли линейныйоператор j, если j(x) = (2 х 1 – х 2, –4 х 1 + 2 х 2).
Решение. Составим матрицу этого линейного оператора: M (j) = 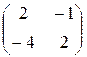 . Так как
. Так как 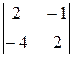 = 0 то матрица M (j) необратима, а значит, необратим и линейныйоператорj.
= 0 то матрица M (j) необратима, а значит, необратим и линейныйоператорj.
2) Найтилинейныйоператор,обратныйоператору j, еслиj(x) = (2 х 1 + х 2, 3 х 1 + 2 х 2).
Решение. Матрица этого линейногооператора, равная M (j) = 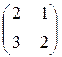 , обратима, так как | M (j)| ≠ 0. (M (j))–1 =
, обратима, так как | M (j)| ≠ 0. (M (j))–1 = 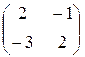 , поэтому
, поэтому
j–1= (2 х 1 – х 2, –3 х 1 + 2 х 2).
9.7. Собственныевекторы линейного оператора
Ввекторном пространстве V над произвольным полем P задан линейныйоператорj.
Определение 9.13. Ненулевой вектор x называется собственным вектором линейного оператора j с собственным значениемλ, если j(х) = λ x.
Говорят, что вектор x принадлежитсобственному значениюλ.
При этомλ называется не только собственным значениемвектора x, но и собственным значением линейного оператора j.
Пример 9.5. 1) Любой ненулевой вектор является собственным вектором оператора гомотетии.
2) Рассмотрим оператор дифференцированиявпространстведифференцируемыхфункций. Вектор f = е 3 х является собственным вектором этого оператора с собственным значением 3, так как f ' = 3 е 3 х = 3 f.
3) Для линейного оператора, заданного матрицей M (j) =  собственнымявляется вектор c = (1, 2, 0), так как j(с) = 2 с. Проверим это:
собственнымявляется вектор c = (1, 2, 0), так как j(с) = 2 с. Проверим это:
[j(с)] = M (j)[ c ] = 
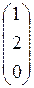 =
= 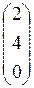 = 2
= 2 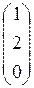 = 2[ с ].
= 2[ с ].
Дата публикования: 2014-11-18; Прочитано: 5654 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
