Абсолютная погрешность результата приближенно равна . Замечание. Если бы d оказалось > 0,005, пришлось бы заново провести расчет с шагом

В результате выполненных шагов получится таблица:

Задание. Вычислить приближенно, пользуясь формулой Симпсона, определенный интеграл , разбивая отрезок интегрирования на 12 равных частей. Затем вычислить интеграл, разбив отрезок интегрирования на 6 частей.

Определить погрешность метода по формуле .

Лабораторная работа №9. Метод Эйлера приближённого интегрирования дифференциального уравнения у' = f (х,у).

Начало численным методам интегрирования задачи Коши дифференциальных уравнений было положено Л. Эйлером в 1768г. В дальнейшем метод Эйлера усовершенствовался и уточнялся. Основной недостаток этих методов – их невысокая точность. Метод Эйлера – одношаговый методы не требуют предварительного построения начала таблицы значений приближенного решения, что дает возможность проводить вычислительный процесс с естественными начальными условиями и переменным шагом...

Рассматриваемые методы приближенного интегрирования ДУ основаны на тождестве:

Пользуясь какой-либо квадратурной формулой для вычисления интеграла, получим различные формулы численного решения ДУ.

Метод Эйлера заключается в том, что интегральную кривую, проходящую через точку (х_оу_о), заменяют ломаной, каждое звено которой

проведено по направлению поля, определённого уравнением у' = f (х,у) в начальной точке этого звена. Иными словами, от предыдущей вершины ломаной к последующей двигаются по касательной к интегральной кривой, проведённой через начальную точку каждого звена.

Предположим, что нас интересует решение, отвечающее отрезку [х_о,b].

Разделим его на п равных частей

тогда ломаная Эйлера определится вершинами

(k= 0, 1, 2,..., п),

где , 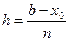- шаг деления,

Расчёт ведётся по следующей схеме:

k
…..	…………	…………	………….	…………..
k
…..
n-1
n

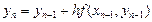
С увеличением числа делений, т.е. с уменьшением шага h, последовательность ломаных Эйлера как угодно близко приближается к искомой интегральной кривой. Но при этом увеличивается время вычислений и возрастает погрешность за счет ошибок округления. На практике задачу решают несколько раз, постепенно уменьшая шаг до тех пор, пока отклонения вычисленных значений функции для одних и тех же значений аргумента не станут пренебрежимо малы с точки зрения вычислителя.

Пример. Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением , при начальном условии y(0)=0, шаг h = 0,1.

Ограничиться отысканием первых 10 значений y.

Ход работы.

1. Включите компьютер, нажмите кнопку Пуск , выберите программу Microsoft Excel.

2. В ячейку A1 введите значение 0.

3. Используя автозаполнение введите значения в ячейки А2 - А6.

4. В ячейки В1 – Е1 введите заголовки:

5. В ячейку В2 введите значение Х_0.

6. В ячейку В3 введите формулу =B2+0,1 и далее продолжите автозаполнением до ячейки В11, заданный шаг h=0,1.

7. В ячейку С3 введите значение y_0.

8. В ячейку С3 введите формулу =C2+0,1*(2*B2-C2) и далее автозаполнением до ячейки С11.

9. В меню Формат ячейки, на вкладке Число выберите Числовой формат, и кол-во знаков после запятой 2. Щелкните ОК.

10. В ячейке D2 вводим: =2*B2-C2 и делаем автозаполнение до D10.

11. В ячейке E2 вводим формулу: =0,1*(2*B2-C2) и делаем автозаполнение до E10

12. Выбираем Формат - Диаграммы. Выберите тип График с накоплением и нажмите Далее.

13. Укажите диапазон от C2 до C11 и ряды в столбцах.

14. Далее выбираем вкладку Ряд. Введите в поле Подписи оси X промежуток от B2 до B11. Нажмите Далее.

15. Сделайте все необходимые подписи к диаграмме. Нажмите Далее.

16. Нажмите Готово.

17.
Для повышения точности расчета уменьшим шаг вычислений. Выполните пп. 1-15 с заданным шагом

Вычисления проводить в ячейках, начиная с F1. Постройте график.

Найдем точное решение данного уравнения:

Данное уравнение является линейным неоднородным дифференциальным уравнением первого порядка.

Общее решение линейного однородного уравнения:

получается разделением переменных

Где С – произвольная постоянная.

Общее решение неоднородного уравнения находим, исходя из общего решения соответствующего однородного уравнения методом Лагранжа, варьируя произвольную постоянную, т.е. полагая:

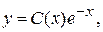где С(x) – некоторая, дифференцируемая функция от x.

Тогда искомое общее решение линейного неоднородного уравнения имеет вид:

Используя начальное условие y(0) = 0, получим:

Следовательно, искомое частное решение имеет вид:

. (*)

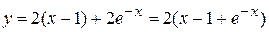График точного решения имеет вид:

Для построения графика точного решения в ячейку Е2 введите формулу (*), используйте автозаполнение. По данным столбца Е постройте график, сравните приближенное решение дифференциального уравнения с точным.

По таблице 1 сравните приближенное значение функции y с точным решением в зависимости от величины шага h.

Таблица 1.