Б. Теорема об изменении количества движения

Количеством движения материальной точки называется произ­ведение массы точки на ее скорость, т.е. вектор .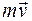

Количеством движения механической системы называется вектор, равный сумме количеств движения точек системы.

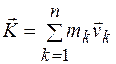, (11.6)

Количество движения системы связано со скоростью ее центра масс соотношением

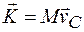, (11.7)

Формулы (11.6) и (11.7) используются при вычислении количест­ва движения системы в проекциях на координатные оси:

,

.

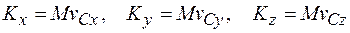Уравнение, описывающее изменение количества движения сис­темы в зависимости от действующих на нее сил, может быть записа­но в двух формах: дифференциальной и интегральной (конечной).

Теорема об изменении количества движения в дифференциаль­ной форме имеет вид

, (11.9)

т.е. производная по времени от количества движения системы равна главному вектору всех внешних сил системы.

Теорема об изменении количества движения в интегральной форме имеет вид

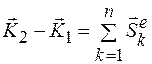, (11.9)

где 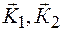- количества движения системы в моменты t ₁ и t ₂; 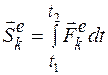- импульс силы за время t ₂ –t ₁.

При решении задач равенства (11.8) и (11.9) используются в проекциях на координатные оси:

.

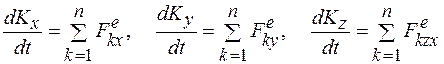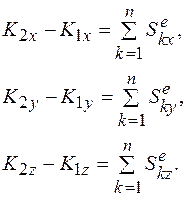
Проекции импульса силы определяются по формулам

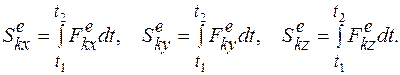
Следствия из теоремы:

1. Если главный вектор внешних сил, действующих на систему, равен нулю: 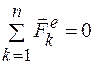, то из (11.8) следует, что

,

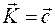т.е. количество движения системы не изменяется при ее движении.

2. Если проекция главного вектора внешних сил на какую-либо ось, например х, равна нулю, т.е. 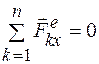, то проекция количества движения системы на эту ось не изменяется при ее движении:

.

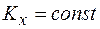Все многообразие задач, которые могут быть решены с помо­щью теоремы о движении центра масс и теоремы об изменении ко­личества движения, можно разделить на два типа:

1. Задачи, в которых движение центра масс системы известно; требуется определить неизвестную внешнюю силу, как правило, это реакция одной из связей.

2. Задачи, в которых имеет место сохранение движения центра масс в проекции на одну из осей. Искомыми величинами могут быть уравнение движения, скорость, перемещение какого-либо тела системы и т.п.

Рассмотрим порядок решения указанных задач.