А. Теорема о движении центра масс

Центром масс механической системы называется геометрическая точка С про­странства, определяемая радиус-вектором

,

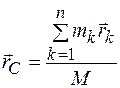где 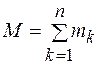- масса системы.

Координаты центра масс определяются по формулам:

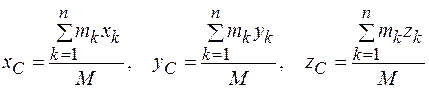, 3(.2)

где x_k, y_k, z_k - координаты точки М_к.

Движение центра масс описывается уравнением

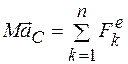, (11.1)

в котором 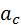- ускорение центра масс, 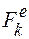- внешняя сила, дейст­вующая на точку М_k.

Формула (11.1) выражает теорему о движении центра масс:

Центр масс механической системы движется как матери­альная точка, в которой сосредоточена масса системы и к ко­торой приложены все внешние силы, действующие на систему.

При решении конкретных задач теорема о движении центра масс используется в проекциях на координатные оси:

(11.2)

Здесь х_с, у_с, z_с - проекции ускорения центра масс, a 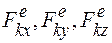проекции силы .

Следствия из теоремы:

1. Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. 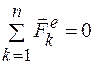, то из (11.1) при этом следует, что 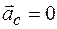или

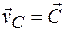, (11.3)

где 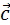- постоянный вектор, т.е. центр масс системы движется рав­номерно и прямолинейно.

2. Если проекция главного вектора внешних сил на какую-либо ось, например х, равна нулю, т.е. 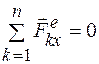, то проекция скорости центра масс на эту ось не изменяется при движении системы:

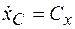. (11.4)

Выражение (11.4) мож­но переписать в виде

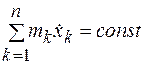. (11.5)