Базовые понятия теории и методические рекомендации по решению задач. Движение материальной точки массы т под действием систе­мы сил ( ), происходящее относительно инерциальной системы отсчета

Движение материальной точки массы т под действием систе­мы сил (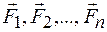), происходящее относительно инерциальной системы отсчета, описывается уравнением

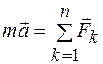, (10.1)

где 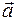- ускорение точки. Если точка является несвободной, то в правую часть соотношения (10.1) входят также реакции связей.

Поскольку 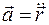, где 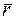- радиус-вектор точки, то уравнение (10.1) можно записать в виде

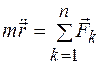. (10.2)

Уравнение (10.2) называется дифференциальным уравнением движения материальной точки в векторной форме. При решении конкретных задач динамики материальной точки уравнение (10.2) записывается соответственно избранной системе координат.

Дифференциальные уравнения движения материальной точки в проекциях на оси прямоугольной декартовой системы координат имеют вид

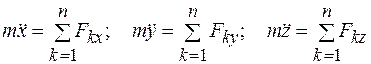, (10.3)

здесь 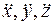- проекции ускорения точки, a 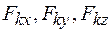- проекции силы 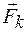на соответствующие оси координат.

Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трехгранника записываются в форме

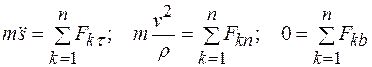, (10.4)

где s - дуговая координата; 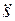- касательное уско­рение точки; v - модуль скорости; ρ - радиус кривизны траектории в данной точке; 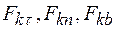- проекции силы 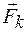на касательную τ, главную нормаль п и бинормаль b соответственно.

С помощью дифференциальных уравнений движения матери­альной точки можно решать первую и вторую задачи динамики.

Первая (прямая) задача. Зная закон движения и массу точки, определить силу, действующую на точку.

Для решения этой задачи необходимо знать ускорение точ­ки. В задачах этою типа оно может быть задано непосредственно либо задан закон движения точки, в соответствии с ко­торым оно может быть определено.

Если движение свободной материальной точки массы т за­дано в прямоугольных декартовых координатах x=x (t), y=y (t), z = z(t), то первая задача динамики решается в следующем порядке:

1. Определяются проекции силы на оси х, у и z по формулам

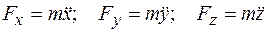. (10.5)

2. Вычисляется модуль силы

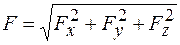. (10.6)

3. Определяется направление силы с помощью направляющих косинусов

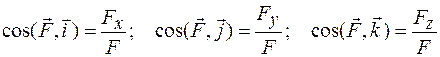. (10.7)