 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение. Воспользуемся формулой
|
|
Воспользуемся формулой 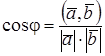 .
.
 ;
;



Векторное произведение векторов
Векторным произведением вектора 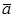 на вектор
на вектор  называется вектор
называется вектор  , обозначаемый символом
, обозначаемый символом 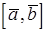 (или
(или 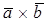 ) и определяемый тремя правилами:
) и определяемый тремя правилами:
1.  , где
, где  угол между векторами
угол между векторами 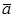 и
и  ;
;
2. вектор  перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов 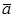 и
и  ;
;

|
3. вектор  ориентирован так, что если смотреть с его конца на плоскость векторов
ориентирован так, что если смотреть с его конца на плоскость векторов 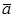 и
и  , то кратчайший поворот от
, то кратчайший поворот от 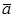 к
к  происходит против часовой стрелки (см. рис.)
происходит против часовой стрелки (см. рис.)
Алгебраические свойства векторного произведения:
1)  ;
;
2)  , где
, где  вещественное число;
вещественное число;
3)  .
.
Геометрические свойства векторного произведения:
1) модуль векторного произведения  равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах 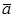 и
и  ;
;
2) если  ,
,  , то
, то  тогда и только тогда, когда
тогда и только тогда, когда 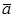 и
и  параллельные векторы;
параллельные векторы;
3) если векторы 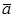 и
и  заданы декартовыми координатами
заданы декартовыми координатами  ,
,  , то векторное произведение
, то векторное произведение 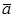 на
на  вычисляется по формуле
вычисляется по формуле
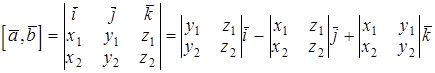 .
.
Пример. Даны точки  ,
,  ,
, 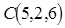 . Вычислить площадь треугольника
. Вычислить площадь треугольника  .
.
Дата публикования: 2014-11-18; Прочитано: 270 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
