Взаимное расположение прямых

Всякое уравнение первой степени относительно 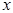и 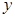, т. е. уравнение вида

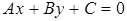, (6)

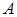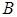где , и 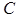- постоянные коэффициенты, причем 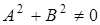, определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.

Если в общем уравнении прямой 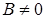, то разрешив его относительно 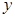, получим уравнение прямой с угловым коэффициентом

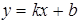, (7)

где 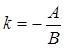- тангенс угла, образованного прямой с положительным направлением оси 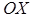; 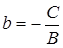- ордината точки пересечения прямой с осью .

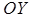Уравнение 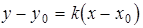(8)

является уравнением прямой, которая проходит через точку 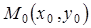и имеет угловой коэффициент .

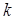Если в общем уравнении прямой 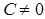, то, разделив все члены на 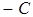, получим уравнение прямой «в отрезках»

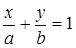, (9)

где 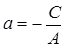, 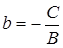– величины направленных отрезков, отсекаемых прямой на осях координат 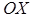и 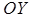, соответственно.