Уравнение

, (10)

является уравнением прямой, проходящей через две точки и .

Обозначим , координаты направляющего вектора прямой , тогда (10) примет вид

, (11)

где 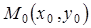– точка на прямой. Уравнение (11) называется каноническим уравнением прямой. Введя параметр , из (10) получим параметрические уравнения прямой

где (12)

Уравнение прямой, проходящей через точку 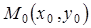перпендикулярно вектору , имеет вид

. (13)

Вектор – называется нормальным вектором прямой. Раскрывая в (13) скобки, получим общее уравнение прямой

.

Таким образом, в общем уравнении прямой, коэффициенты пр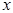и и 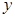суть координаты нормального вектора прямой.

Пусть две прямые заданы уравнениями с угловыми коэффициентами и . Возможны следующие случаи их взаимного расположения:

1) прямые параллельны (в частности совпадают) тогда и только тогда, когда выполняется условие ;

2) прямые пересекаются в некоторой точке, тогда угол между ними находится по формуле ;

3) прямые перпендикулярны тогда и только тогда, когда .

Пример. В равнобедренном прямоугольном треугольнике даны декартовы координаты вершины острого угла и уравнение противолежащего катета . Составить уравнения двух других сторон этого треугольника.