Решение. Выпишем расширенную матрицу и приведем ее к треугольному виду (4):

Выпишем расширенную матрицу и приведем ее к треугольному виду (4):

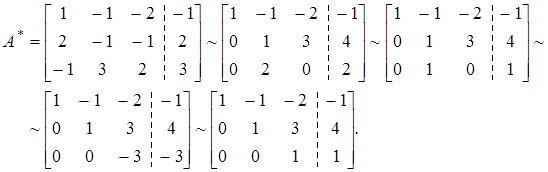
Разберем преобразование матрицы :

1) ко второй строке прибавим первую, умноженную на 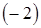, к третьей строке прибавим первую;

2) сократим третью строку на ;

3) к третьей строке прибавим вторую, умноженную на ;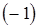

4) сократим третью строку на .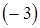

Мы видим, что 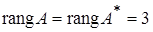, т. к. базисный минор 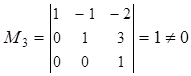. Число неизвестных 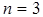. Следовательно, система совместна и имеет единственное решение. Найдем его методом Гаусса, для этого запишем систему, соответствующую преобразованной матрице 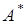(укороченная система):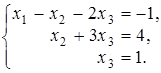

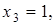
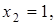
Откуда получим: 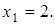Проверка: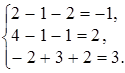

Ответ: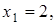

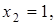
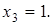
СХЕМА РЕШЕНИЯ ПРОИЗВОЛЬНОЙ СИСТЕМЫ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

1) проверяем условие 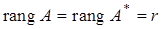(если 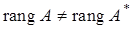, то система не имеет решения);

2) выбираем базисный минор порядка 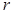и записываем укороченную систему;

3) неизвестные 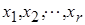назовем базисными, а свободными и выразим базисные неизвестные через свободные;

4) записываем общее решение системы.

Пример. Найти общее решение однородной системы линейных уравнений и одно частное решение

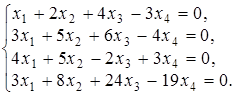
Однородная система всегда совместна, т.к. ее расширенная матрица 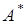получается добавлением к основной матрице 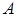нулевого столбца и, следовательно, всегда .

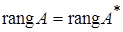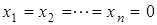всегда является решением однородной системы (тривиальное решение).

Для существования нетривиального (ненулевого) решения однородной системы необходимо и достаточно, чтобы .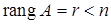

Найдем ранг матрицы .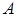

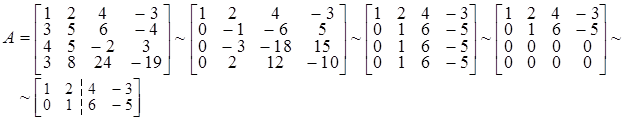
Разберем преобразования матрицы :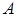

1) ко второй строке прибавим первую, умноженную на 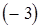, к третьей строке прибавим первую, умноженную на 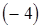, к четвертой строке прибавим первую, умноженную на ;

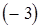2) разделим элементы второй строки на 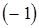, элементы третьей строки на 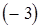, а элементы четвертой строки на 2;

3) из третьей и четвертой строк вычтем вторую строку.