Решение. Скалярное произведение векторов, его свойства

а) ;

Скалярное произведение векторов, его свойства

Скалярным произведением двух векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними. Скалярное произведение векторов и обозначается или .

Обозначим через угол между векторами и . Тогда скалярное произведение выражается формулой

.

Если векторы 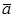и заданы декартовыми координатами , , то скалярное произведение вычисляется по формуле

.

Скалярное произведение векторов и равно нулю (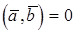) тогда и только тогда, когда векторы и перпендикулярны. В частности 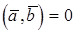, если или .

Алгебраические свойства скалярного произведения:

1.

2. , где константа;

3. .

С помощью скалярного произведения можно вычислить:

1. Модуль вектора : . Эта формула справедлива для любой системы координат. В частности, в декартовой системе координат данная формула примет вид , где .

2. Косинус угла между векторам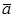и и

.

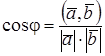3. Проекцию вектора 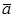на вектор

.

Пример. Вектор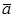ы и взаимно перпендикулярны и , . Найти .