 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Операції піднесення до степеня
|
|
Поняття цілого степеня комплексного числа 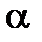 вводиться так само як і для дійсного числа. Нагадаємо, що
вводиться так само як і для дійсного числа. Нагадаємо, що 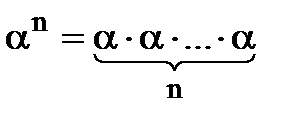 при
при 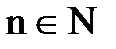 .
.
Домовились вважати 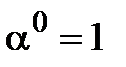 . Для введення
. Для введення 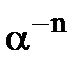 існують два шляхи.
існують два шляхи.
1)  , де
, де 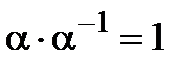
2) 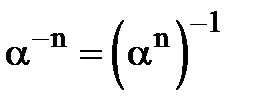
Для корректності введеного поняття треба виконати вправу:
1) Довести
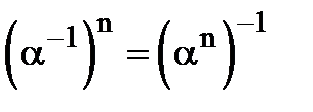
2) Довести 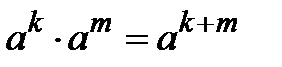 при
при 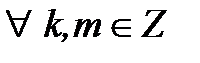 .
.
1. Розглянемо спочатку операцію піднесення в алгебраїчній формі. Нехай задано число 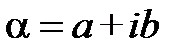 . Оскільки з попередніх означень випливає, що піднесення до цілого степеня зводиться до піднесення до натурального степеня, то можна скористатися формулою Бінома Ньютона:
. Оскільки з попередніх означень випливає, що піднесення до цілого степеня зводиться до піднесення до натурального степеня, то можна скористатися формулою Бінома Ньютона:
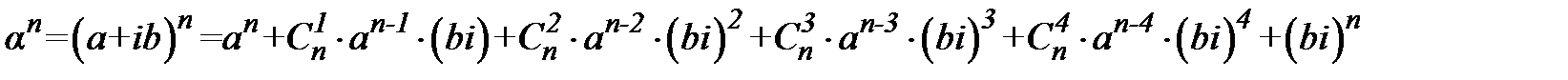
Розглянемо таблицю множення числа і
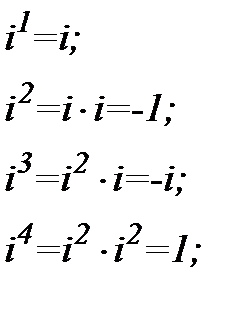 з цього випливає
з цього випливає 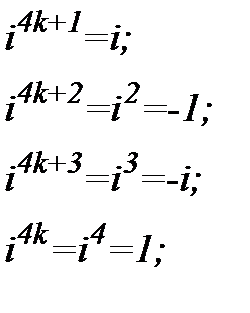
Використовуючи таблицю множення та виділяючи дійсну та уявну частину, отримаємо
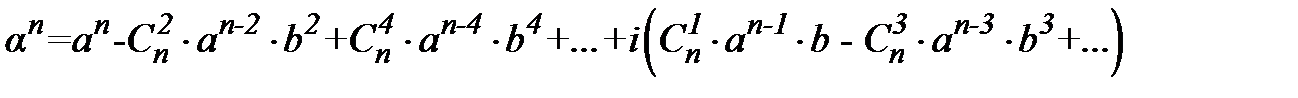
| (1) |
2. Розглянемо операцію піднесення до степеню, коли  задано в тригонометричній формі.
задано в тригонометричній формі.
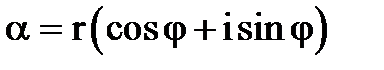
Використовуючи правило множення комплексних чисел в тригонометричній формі, маємо
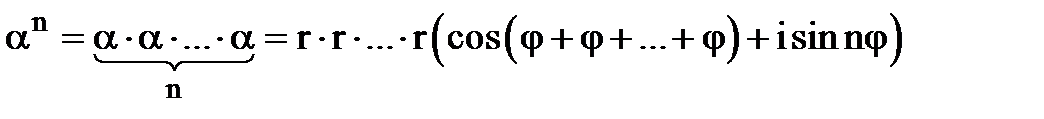 .
.
Тобто, 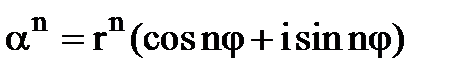 - формула Муавра - формула Муавра
| (2) |
Застосуємо отримані рівності (1) і (2) для знаходження розкладання 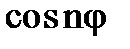 і
і 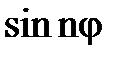 через
через 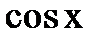 і
і  . Окремі випадки цих формул при n=2,3 відомі зі шкільного курсу.
. Окремі випадки цих формул при n=2,3 відомі зі шкільного курсу.
Застосуємо до числа 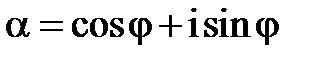 формулу (2). В тригонометричній формі
формулу (2). В тригонометричній формі 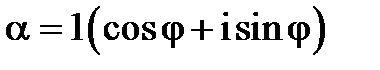
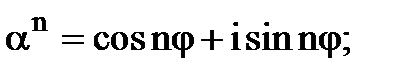 (3)
(3)
Застосуємо формулу (1) при 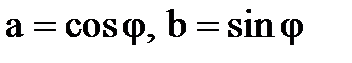 , отримаємо
, отримаємо
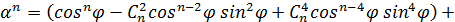
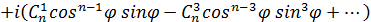
Порівнюючи в формулах (3) і (4) дійсні та уявні частини, отримаємо

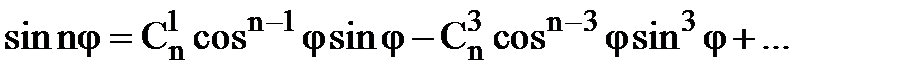 (4)
(4)
Дата публикования: 2014-11-18; Прочитано: 891 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
