 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Полярна система координат
|
|
Означення. Полярною системою координат називають систему координат на площині, що складається з числової прямої, яка називається полярною віссю і точки на ній, що називається полюсом.
| φ |
| М |
Якщо ввести полярну систему координат, то положення точки М на площині визначається довжиною її радіуса-вектора  і кутом між полярною віссю і радіусом-вектором
і кутом між полярною віссю і радіусом-вектором  .
.
Як завжди, додатній кут отримується поворотом проти годиникової стрілки. Якщо задані r та j, то точка визначається однозначно на пллощині. Якщо ж задати точку, то r визначається однозначно, а j - неоднозначно, а з точністю до доданка 2kπ.
Для того, щоб ліквідувати таку неоднозначність, домовимось, розглядати кут в межах 0 £ p £ 2 або -p £ j £ p. Тоді виникає взаємнооднозначна відповідність між точками площини і числами r та j.
Означення. Числа r та j називаються полярними координатами точки. Число r – полярним радіусом, кут j - полярним кутом точки М.
Знайдемо зв¢язок між полярними координатами точки і декартовими прямокутними. Введемо декартову прямокутну систему координат таким чином, що її початок збігається з полюсом, а вісь Ох з полярною вісью.
Використовуючи теорему про геометричний зміст декартових прямокутних координат, маємо
| φ |
| φ |
| M |
| M |
| x |
| x |
| y |
| y |
 j.
j. 
 (90°-j) = r× sinj.
(90°-j) = r× sinj.
Якщо відомі r та j, то x і y можна обчислити за формулами
x = r cos j
y = r sin j.
Поставимо обернену задачу: відомі x та y, треба знайти r та j.
З попередніх рівностей маємо:

З цих рівностей випливає
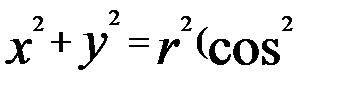 j+
j+  j),
j),
 ,
,  ,
,
 j
j  ,
, 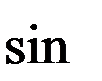 j
j 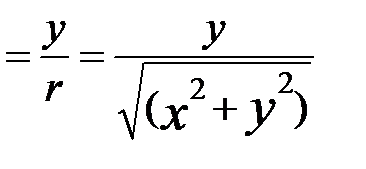 .
.
Дата публикования: 2014-11-18; Прочитано: 541 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
