Корені n-ого степеня з одниці

Застосуємо отриману формулу в окремому випадку при 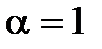. Подамо 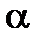в тригонометричній формі:

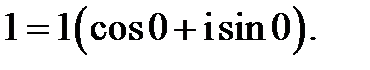
Тоді,

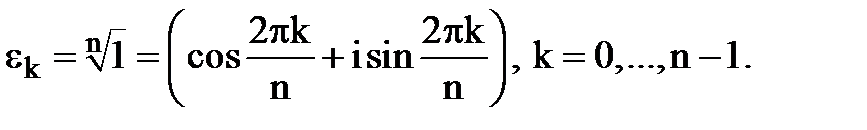
Корені 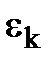n-ого степеня з 1 мають цікаві властивості.

Властивість 1 Добуток двох коренів n-ого степеня з одиниці є також коренем n-ого степеня з одиниці.

Доведення. Нехай 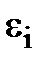та 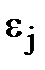- корені n-ого степеня з одиниці, тобто 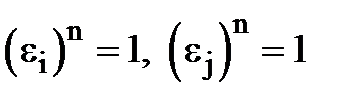. Треба довести, що 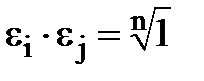, тобто що .

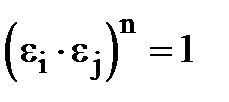Розглянемо

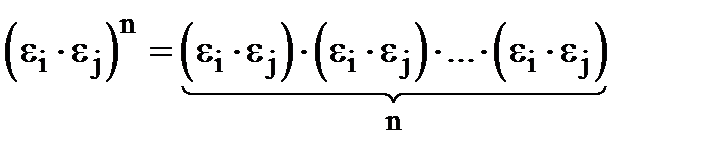
Внаслідок асоціативності і комутативності множення комплексних чисел маємо

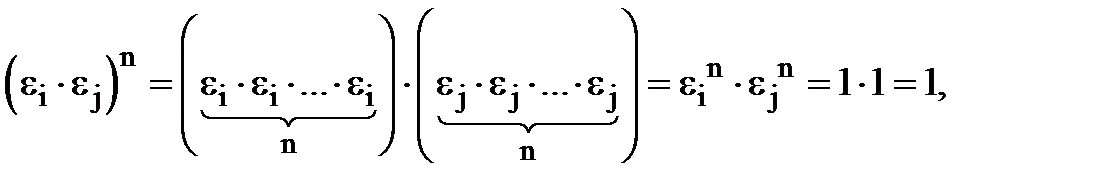
що і треба було довести.

З цієї властивості випливає наслідок.

Наслідок 1. Будь-який натуральний степінь кореня n-ого степеня з одиниці є також коренем n-ого степеня з одиниці.

Властивість 2 Число обернене до кореня n-ого степеня з одиниці є також коренем n-ого степеня з одиниці.

Доведення. Нехай 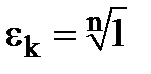, 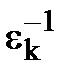- число обернене до 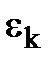, тому 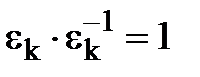. Треба довести, що 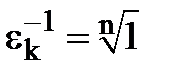, тобто .

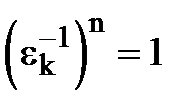Розглянемо 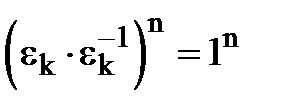. Звідси внаслідок коммутативності і ассоциативності множення маємо 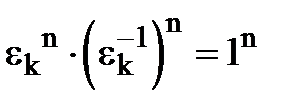. Оскільки 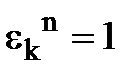, то 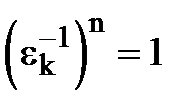, що і треба було довести.

Наслідок 2. Будь-який від`ємний степінь кореня n-ого степеня з одиниці є також коренем n-ого степеня з одиниці.

Це випливає з того, що .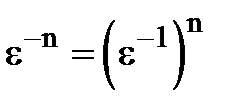

Оскільки 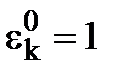, то з наслідків 1 та 2 випливає: будь-який цілий степінь кореня n-ого степеня з одиниці також є коренем n-ого степеня з одиниці.

В подальшому ці властивості в розділі теорії груп дозволять побудувати мультиплікативну групу коренів n-ого степеня з одиниці.

Розглянемо властивість, важливу з практичної точки зору.

Властивість 3. Добуток кореня n-ого степеня з числа 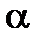на корінь n-ого степеня з одиниці є коренем n-ого степеня з числа .

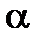Доведення. Нехай 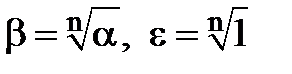. Треба довести, що 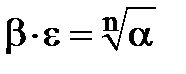, тобто що .

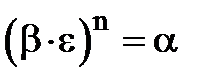Розглянемо 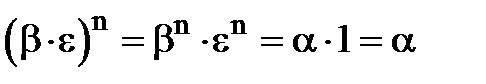, що і треба було довести.

З цієї властивості випливає, що всі корені n-ого степеня з числа 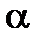можна отримати помноживши одного з них на кожний корінь n-ого степеня з одиниці.